Flocking for Networks of Mobile Robots with Nonlinear Dynamics
Reza Olfati-Saber and Lamia Iftekhar
Dartmouth College, Hanover, NH 03755, U.S.A.
Keywords:
Flocking, Nonholonomic Robots, Multi-robot Networks, Near-Identity Transformation, Nonlinear Systems.
Abstract:
In this paper, we address the problem of flocking for networks of nonholonomic mobile robots with nonlinear
dynamics given that a flocking algorithm for particles is known. Our approach relies on the use of near-identity
change of coordinates that transform the nonlinear dynamics of the robot to a partially-linear normal form with
a double-integrator linear subsystem. The flocking algorithm is then applied to the linear part. The inverse
of the near-identity transformation provides the flocking algorithm for the networked nonholonomic robots.
We prove the emergence of flocking behavior for robotic networks with nonlinear dynamics according to the
formal definition of flocking in Olfati-Saber’s flocking paper (TAC ’06). Simulation results are provided for
large-scale networks of two-wheeled robots with nonlinear dynamics as models of Khepera-III robots that
demonstrate the effectiveness of our proposed transformation and algorithm.
1 INTRODUCTION
Flocking is a form of collective behavior of a large
number of interacting mobile agents with a uni-
fied objective (e.g. moving towards the same di-
rection) with an elegant lattice shaped spatial or-
der that reflects cohesive group motion (Olfati-Saber,
2006). Group behaviors such as flocking, school-
ing, and herding are one of the few research sub-
jects that are of great interest to physicists (Vicsek
et al., 1995; Shimoyama et al., 1996; Toner and Tu,
1998; Levine et al., 2001), computational social sci-
entists (Helbing et al., 2000), animal behavior experts
(Shaw, 1975; Potss, 1984; Partridge, 1982; Parrish
et al., 2002), applied mathematicians (Mogilner and
Edelstein-Keshet, 1999; Topaz and Bertozzi, 2004;
D’Orsogna et al., 2006; Cucker and Smale, 2007),
computer scientists (Reynolds, 1987), and robotics
and control scientists (Olfati-Saber, 2006) alike.
Some of the existing results on flocking and for-
mation control for groups of nonholonomic agents
can be found in (Regmi et al., 2005; Dimarogonas
and Kyriakopoulos, 2006a; Dimarogonas and Kyr-
iakopoulos, 2006b; Dimarogonas and Kyriakopou-
los, 2007; Moshtagh and Jadbabaie, 2007; Dong and
Farrell, 2008; Chopra et al., 2008; Tanner et al.,
2005). In this paper, we extend the flocking algo-
rithms from (Olfati-Saber, 2006) for groups of parti-
cles with double-integrator dynamics ¨q
i
= u
i
to mo-
bile robots with nonlinear dynamics. We address
the problem of flocking for networked nonholonomic
robots with nonlinear dynamics shown in Fig. 1.
Our approach to flocking for dynamic nonholo-
nomic robots relies on application of near-identity dif-
feomorphisms (Olfati-Saber, 2002) that transform the
nonlinear dynamics of the robot into a partially-linear
normal form with a double-integrator linear part and
applying the flocking algorithm to the reduced normal
form. The flocking algorithm for the original network
of mobile robots can be obtained using the inverse of
the near-identity diffeomorphism.
The aforementioned reduction method is more
general and can be applied to the design of flocking al-
gorithms for other types of mobile robots with nonlin-
ear dynamics if the corresponding near-identity trans-
formation of the robot can be found. The main chal-
lenge is to prove that the resulting flocking algorithm
for robotic networks with nonlinear dynamics leads
to emergence of flocking behavior according to the
formal definition of flocking in (Olfati-Saber, 2006).
Establishing the emergence of flocking is one of our
main results.
Here is an outline of the paper: Some background
and notation on flocking are provided in Section 2.
The nonholonomic robot and its dynamics are pre-
sented in Section 3, which also details a coordinate
change using near identity diffeomorphism. Our main
theoretical result is presented in Section 5. Simulation
results are provided in Section 6. Finally, concluding
remarks are made in Section 7.
353
Olfati-Saber R. and Iftekhar L..
Flocking for Networks of Mobile Robots with Nonlinear Dynamics.
DOI: 10.5220/0004048403530359
In Proceedings of the 9th International Conference on Informatics in Control, Automation and Robotics (ICINCO-2012), pages 353-359
ISBN: 978-989-8565-22-8
Copyright
c
 2012 SCITEPRESS (Science and Technology Publications, Lda.)

2 FLOCKING ALGORITHMS
FOR PARTICLES
In this section, we provide some background and no-
tations on Olfati-Saber’s flocking algorithms and the-
ory (Olfati-Saber, 2006). Consider a group of n parti-
cles called α-agents moving in R
m
with the following
dynamics

˙q
i
= p
i
˙p
i
= u
i
(1)
where q
i
, p
i
,u
i
∈ Rm denote the position, velocity,
and control of agent i, respectively. Let us denote the
conformation of all α-agents by q = col(q
1
,...,q
n
) ∈
R
mn
. The proximity network of the agents is a dy-
namic graph G(q) = (V,E(q)) with the set of nodes
V = {1,2,...,n} and the set of edges
E(q) = {(i, j) ∈V ×V : kq
j
−q
i
k ≤ r}.
The adjacency matrix of G(q) is a non-negative
matrix A(q) = [a
i j
(q)] with smooth elements 0 ≤
a
i j
(q) ≤ 1 defined in (Olfati-Saber, 2006). The set of
neighbors of agent i is defined as N
i
(q) = {j : (i, j) ∈
E(q)}. A conformation q is called a quasi α-lattice if
every agent is approximately equally distanced from
all of its neighbors, i.e.
∃ε,d > 0 : −ε ≤ kq
j
−q
i
k−d ≤ ε, ∀j ∈N
i
(q).
An α-lattice is a quasi α-lattice with ε = 0. The for-
mal definition of flocking is given in (Olfati-Saber,
2006) as follows:
Definition 1. (flocking) A group of α-agents with the
trajectory (q(·), p(·)) perform flocking behavior over
a time interval [t
0
,t
f
), if every agent i only communi-
cates with its neighbors N
i
and the trajectories of the
agents satisfy the following properties over the period
[t
0
,t
f
):
1. Cohesion: ∃ρ > 0 : kq
i
(t)−q
c
(t)k≤ρ and q
c
(t) =
1
n
∑
n
i=1
q
i
(t).
2. Self-assembly of a quasi α-lattice after some finite
time;
3. Self-assembly of a connected proximity network
G(q(t)) after some finite time;
4. Self-alignment: a relatively small velocity mis-
match
∃0 < ε 1 : K(p) =
1
2
∑
(i, j)∈E(q)
kp
j
(t)−p
i
(t)k
2
< ε
It is shown in (Olfati-Saber, 2006) that Algorithm
2 leads to emergence of flocking behavior. This flock-
ing algorithm can be described as follows:
u
i
= f
α
i
+ f
γ
i
(2)
or in a more explicit form, it can be expressed as
u
i
=
∑
j∈N
i
φ
α
(kq
j
−q
i
k
σ
)n
i j
| {z }
gradient-based term
+
∑
j∈N
i
a
i j
(q)(p
j
−p
i
)
| {z }
consensus term
+ f
γ
i
(3)
where n
i j
= (q
j
−q
i
)/
p
1 + εkq
j
−q
i
k
2
is a bounded
vector along the line connecting q
i
to q
j
and ε ∈
(0,1). Moreover ksk
σ
=
1
ε
(
p
1 + εksk
2
−1) denotes
the σ-norm of vector s.The potential function of the
group is defined as V (q) =
∑
j6=i
ψ
α
(kq
j
−q
i
k
σ
) where
ψ
α
(s) =
R
s
kdk
σ
φ
α
(h)dh. The scalar function φ
α
(s) is
defined in eq. (15) of (Olfati-Saber, 2006). f
γ
i
is a
linear tracking controller
f
γ
i
= −c
γ
1
(q
i
−q
r
) −c
γ
2
(p
i
−p
r
); c
γ
1
,c
γ
2
> 0 (4)
where (q
r
, p
r
) is the state of the γ-agent, i.e. a vir-
tual moving rendezvous point (with double integrator
dynamics). The objective of all α-agents is to asymp-
totically track a single γ-agent (or common goal).
In the presence of obstacles, Algorithm 3 in
(Olfati-Saber, 2006) is applicable. Let us refer to the
projection of an α-agent on the boundary of a con-
vex obstacle (e.g. a wall, or an ellipse) as a β-agent.
Obstacle avoidance can be achieved by establishing a
repulsive potential between an α-agent and its β-agent
projection on a neighboring obstacle. The flocking al-
gorithm with obstacle avoidance capabilities is in the
form
u
i
= f
α
i
+ f
β
i
+ f
γ
i
(5)
where f
β
i
is the obstacle avoidance force and is given
by
f
β
i
= c
β
1
∑
k∈N
β
i
φ
β
(kˆq
i,k
−q
i
k
σ
)
ˆ
n
i,k
+ c
β
2
∑
j∈N
β
i
b
i,k
(q)( ˆp
i,k
−p
i
); c
β
1
,c
β
2
> 0
(6)
Here, ˆq
i,k
and ˆp
i,k
with (i,k) ∈V
α
×V
β
denote the po-
sition and velocity of a β-agent generated by an α-
agent with state (q
i
, p
i
) on an obstacle. The functions
b
i,k
(q) and φ
β
(s) are defined in equations (55) and
(56) respectively of (Olfati-Saber, 2006) and
ˆ
n
i,k
=
( ˆq
i,k
−q
i
)/
p
1 + εkˆq
i,k
−q
i
k
2
Consider a wall obsta-
cle (a hyperplane) with a unit normal a
k
passing
through a point y
k
. The projection matrix for this ob-
stacle is P = I −a
k
a
T
k
. The position and velocity of
the β-agent are given by
ˆq
i,k
= Pq
i
+ (I −P)y
k
, ˆp
i,k
= Pp
i
. (7)
ICINCO2012-9thInternationalConferenceonInformaticsinControl,AutomationandRobotics
354

3 NONHOLONOMIC ROBOT
AND TRANSFORMATION
In this section, we study a two-wheeled mobile robot
with nonlinear dynamics shown in Fig. 1 that can
be used as the model of commercial robots such
as Khepera-III. After presenting the nonlinear dy-
namics of the mobile robot, we will demonstrate
how the robot dynamics can be transformed into a
partially-linear system using near-identity diffeomor-
phisms (Olfati-Saber, 2002) where the linear part is a
particle model (double integrator) and therefore flock-
ing algorithms are applicable to the transformed sys-
tem. Inversion of the transformation provides flock-
ing algorithms for networked mobile robots with non-
linear dynamics.
𝜃
(𝑥
1
, 𝑥
2
)
𝑥
𝑦
𝑓
2
𝑓
1
Figure 1: Configuration variables and controls of a two-
wheeled mobile robot.
3.1 Dynamics of the Mobile Robot
Fig. 1 shows a two-wheeled mobile robot with the fol-
lowing nonlinear dynamics















˙x
1
= v cos θ
˙x
2
= v sin θ
˙
θ = ω
m ˙v = f
1
+ f
2
J
˙
ω = ¯r( f
1
− f
2
)
(8)
where (x
1
,x
2
)
T
∈ R is the position of the center of
mass, θ is the orientation angle of the robot, f
1
and f
2
are control forces and m, J, and ¯r, are mass, moment
of inertia, and half of the length of the wheel-base.
Defining the following change of control

u
1
= ( f
1
+ f
2
)/m
u
2
= ¯r( f
1
− f
2
)/J
(9)
the dynamics of the robot in (8) can be rewritten as
( ˙x
1
, ˙x
2
,
˙
θ, ˙v,
˙
ω) = [v cos θ, v sin θ, ω, u
1
,u
2
]
T
(10)
Notice that for all t ∈ R, the velocities ˙x
1
and ˙x
2
satisfy the following first-order nonholonomic con-
straint
˙x
2
cosθ − ˙x
1
sinθ = 0 (11)
Denoting x = (x
1
,x
2
)
T
, one can write the dynamics of
the robot in a coordinate-independent manner as









˙x = (Re
1
)v
˙v = u
1
˙
R = R
ˆ
ω
˙w = u
2
(12)
where e
1
= (1,0)
T
, e
2
= (0,1)
T
, Re
k
is the kth column
of R ∈ SO(2) for k = 1,2 and
R =

cosθ −sin θ
sinθ cosθ

,
ˆ
ω =

0 −ω
ω 0

(13)
3.2 Near-identity Transformation
The dynamics of the nonholonomic mobile robot
in (12) can be transformed into a cascade of a
double-integrator and attitude dynamics. This can be
performed using a nonlinear change of coordinates
called a near-identity transformation and introduced
in (Olfati-Saber, 2002). This transformation is given
by
z = x + λ(Re
1
) (14)
where λ is relatively small constant.
By direct differentiation, we get
˙z = ˙x + λ(
˙
Re
1
)
= (Re
1
)v + λ(R
ˆ
ωe
1
)
= (Re
1
)v + λω(Re
2
)
= R
λ
p
(15)
with p = (v,ω)
T
∈ R
2
and R
λ
= [(Re
1
)|λ(Re
2
)]. The
matrix R
λ
can be explicitly expressed as
R
λ
=

cos(θ) −λsin(θ)
sin(θ) λcos(θ)

(16)
Clearly , det(R
λ
) = λ and thus R
λ
is an invertible
matrix if and only if λ 6= 0. For λ 6= 1, R
λ
is not a
SO(2) matrix. Notice that ˙p = u, thus
¨z = R
λ
u +
˙
R
λ
p = τ (17)
where τ is the new control input for the linear system
¨z = τ. (18)
To find an explicit relation between u and τ , we
need to calculate
˙
R
λ
p as follows
FlockingforNetworksofMobileRobotswithNonlinearDynamics
355

˙
R
λ
p = [R
ˆ
ωe
1
|λR
ˆ
ωe
2
].(v,ω)
T
= [ωRe
2
|−λωRe
1
](v, ω)
T
= vωRe
2
−λω
2
Re
1
= R(−λω
2
,vω)
T
(19)
Hence, u = (u
1
,u
2
)
T
can be obtained as
u = R
−1
λ
τ −R
−1
λ
R(λω
2
,vω)
T
(20)
On the other hand, we have
R
−1
λ
R =
"
1 0
0
1
λ
#
(21)
thus
u = R
−1
λ
τ +
"
λω
2
−vω
λ
#
(22)
The complete dynamics of the mobile robot in
new coordinates in given by











˙z = w
˙w = τ
˙
R = R
ˆ
ω
˙
ω = e
T
2
u = e
T
2
R
−1
λ
τ −
vω
λ
(23)
with a partially-linear (z,w)-subsystem. We apply our
particle-based flocking algorithms to this partially-
linear subsystem of the transformed dynamics of the
mobile robot.
4 FLOCKING FOR NONLINEAR
ROBOTIC NETWORKS
Consider a network of robots with the dynamics in
(8). To implement the flocking algorithm (2) on this
network, we perform a change of coordinates as in
the previous section obtaining the double integrator
for the ith robot

˙z
i
= w
i
˙w
i
= τ
i
(24)
which is the same as the particle dynamics in (1) after
relabeling of the variables. Applying the following
algorithm from (2)
τ
i
= f
α
i
+ f
γ
i
(25)
leads to flocking behavior for networked mobile
robots with nonlinear dynamics. For group motion in
an environment with obstacles, collision-free flocking
behavior is achieved using the application of the algo-
rithm in (5), i.e.
τ
i
= f
α
i
+ f
γ
i
+ f
β
i
(26)
5 ANALYSIS OF FLOCKING FOR
ROBOTIC NETWORKS
Our main result is that if the near-identity transfor-
mation of mobile robots (oriented particles) perform
flocking, then the group of mobile robots perform
flocking as well—given some assumptions. Here is
our main analytical result:
Theorem 1. Consider n mobile robots with nonlin-
ear dynamics given in (12) applying the flocking al-
gorithm (25). After applying a near-identity transfor-
mation

z
i
= x
i
+ λ(R
i
e
1
)
w
i
= v
i
(R
i
e
1
) + λω
i
(R
i
e
2
)
(27)
suppose that the n particles with linear dynamics

˙z
i
= w
i
˙w
i
= τ
i
(28)
perform flocking behavior (as defined in Section 2)
so that the angular velocity of all robots remain uni-
formly bounded, i.e. |ω
i
| ≤
¯
ω. Then, the n mobile
robots with nonlinear dynamics perform flocking be-
havior as well.
Proof. To establish that the mobile robots with non-
linear dynamics perform flocking behavior, we need
to prove that the four conditions of flocking in Defini-
tion 1 are satisfied, particularly, achieving a relatively
small velocity mismatch
K(ν) =
1
2
∑
(i, j)∈E(x)
kν
j
−ν
i
k
2
 1
where ˙x
i
= ν
i
.
Suppose that the particle-based model of the
robots form a cohesive trajectory over the time inter-
val [t
0
,t
f
]) with a cohesion radius of ρ > 0. Then, for
any given λ ≥ 0, a slight perturbation of every par-
ticle x = z −λ(Re1) can be geometrically contained
in a slightly larger ball of radius ρ
ε
= ρ + ε(λ) and
thus the trajectory of the group of mobile robots is
cohesive. Formally, this can be shown by defining a
compact set containing all the balls around n
Note that the topology of the proximity network
of the mobile robots is the same as the proximity
network of their induced particle-based models after
near-identity transformation. Therefore, connectivity
of the latter implies connectivity of the former. This
proves property (3).
We prove that the mobile robots form a quasi α-
lattice if their perturbed particle-based models (near-
identity transformations) form a quasi α-lattice. De-
fine the unit vectors r
i
= R
i
e
1
and s
i
= R
i
e
2
. For a pair
of neighboring robots i and j and a small parameter
ICINCO2012-9thInternationalConferenceonInformaticsinControl,AutomationandRobotics
356

λ > 0, we have
z
i
= x
i
+ λr
i
, z
j
= x
j
+ λr
j
and
kx
j
−x
i
k = k(z
j
−z
i
) + λ(r
j
−r
i
)k
≤ kz
j
−z
i
k+ 2λ ≤ d + (ε + 2λ)
Setting ε
1
= ε + 2λ  1 guarantees that kx
j
−x
i
k ≤
d +ε
1
. Similarly, one can show kz
j
−z
i
k≤kx
j
−x
i
k+
2λ. Hence
kx
j
−x
i
k = kz
j
−z
i
k−2λ
≥ d −(ε + 2λ)
In other words, we get d −ε
1
≤kx
j
−x
i
k≤d + ε
1
, or
the mobile robots form a quasi α-lattice.
Finally, we need to show that if the velocity mis-
match is relatively small (K(w) < ε  1) for the
particle-based models of robots, then the velocity
mismatch for the robots K(ν) will also be relatively
small. Note that the velocities of the particles and
robots satisfy w
i
= ν
i
+λω
i
s
i
where s
i
is a unit vector.
Let n
e
= |E| denote the number of edges of the prox-
imity network G(q)—this is a finite number and equal
to
∑
i
k
i
where k
i
is the degree of node i. We have
K(ν) =
1
2
∑
(i, j)∈E
kν
j
−ν
i
k
2
=
1
2
∑
(i, j)∈E
k(w
j
−w
i
) + λ(ω
j
s
j
−ω
i
s
i
)k
2
≤
1
2
∑
(i, j)∈E
kw
j
−w
i
)k
2
+ 2n
e
λ
2
¯
ω
2
+ 2λ
¯
ω
∑
(i, j)∈E
kw
j
−w
i
k
From the property of p-norms, for any vector ξ ∈R
m
,
kξk
1
≤
√
mkξk
2
which implies
∑
(i, j)∈E
kw
j
−w
i
k ≤
√
n
e
(
∑
(i, j)∈E
kw
j
−w
i
)k
2
)
1
2
≤
√
n
e
ε
Therefore, we obtain a positive upper bound for K(ν)
K(ν) ≤ε + 2
√
n
e
ελ
¯
ω + 2n
e
λ
2
¯
ω
2
≤ (
√
ε +
√
n
e
λ
¯
ω)
2
+ n
e
λ
2
¯
ω
2
 1
because ε, λ  1. The trajectory of the group of mo-
bile robots satisfy all four conditions of flocking be-
havior in Definition 1 and perform flocking if their
near-identity transformations do the same.
6 SIMULATIONS
In this section, we present simulation results for flock-
(a)
(b)
(c)
(d)
Figure 2: Flocking for networked nonholonomic robots
with nonlinear dynamics: Consecutive snapshots of the
proximity structure for n = 100 mobile robots in free-space.
Flocking behavior emerges in (c) and is maintained there-
after.
ing behavior by networks of mobile robots with non-
linear dynamics both in free-space in Fig. 2 and in
presence of wall-shaped obstacles in Fig. 3. Parame-
FlockingforNetworksofMobileRobotswithNonlinearDynamics
357

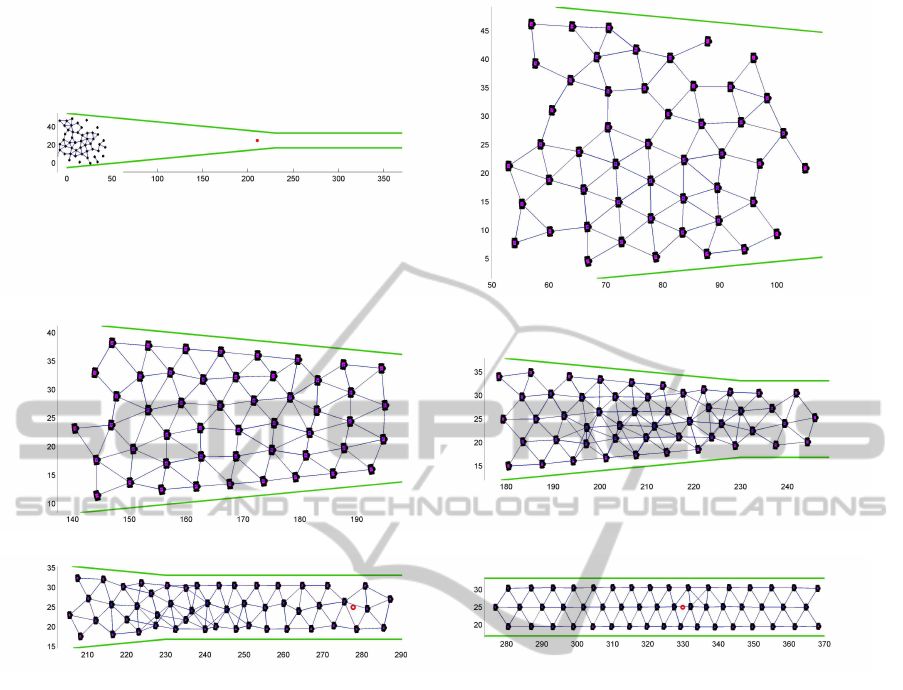
(a) (b)
(c) (d)
(e) (f)
Figure 3: Flocking for networked nonholonomic robots with nonlinear dynamics in presence of wall-shaped obstacles: A
group of n = 50 mobile robots start randomly within the boundaries of two wall-shaped obstacles. As the agents follows a
γ-agent to the right, the space becomes increasingly narrower until the agents are forced to go through a tunnel about one-third
in width compared to that of the initial space. The agents demonstrate squeezing maneuver where they move within a tight
space without collisions: (a) a global view of the obstacles and (b) through (f) consecutive snapshots of the robots as they
move within the boundaries. A quasi α-lattice can be observed in (b), (c), and (f).
ters that are different from those in the flocking sim-
ulations of (Olfati-Saber, 2006) are as follows: a = 5
and b = 10 for φ(z) and λ = 0.25 for the near-identity
transformation.
7 CONCLUSIONS
We addressed the problem of flocking for networks of
nonholonomic robots with nonlinear dynamics given
that a flocking algorithm for particles was known
from (Olfati-Saber, 2006). Near-identity change of
coordinates (Olfati-Saber, 2002) was applied to non-
linear dynamics of the robot to transform it into a
partially-linear normal form with a double-integrator
linear part. Then, the flocking algorithm was ap-
plied to the linear subsystem. The inverse of the
near-identity transformation provides the flocking al-
gorithm for the networked mobile robots with non-
linear dynamics. The approach is more general and
applicable to any partially-linearizable robot dynam-
ics. We proved the emergence of flocking behavior
for robotic networks according to the formal defini-
tion of flocking in (Olfati-Saber, 2006). Simulations
results were provided for large-scale networks of two-
wheeled robots with nonlinear dynamics.
REFERENCES
Chopra, N., Stipanovic, D., and Spong, M. (2008). On
synchronization and collision avoidance for mechani-
cal systems. In American Control Conference, 2008,
pages 3713 –3718.
Cucker, F. and Smale, S. (2007). Emergent behavior in
ICINCO2012-9thInternationalConferenceonInformaticsinControl,AutomationandRobotics
358

flocks. IEEE Trans. on Automatic Control, 52(5):852–
862.
Dimarogonas, D. and Kyriakopoulos, K. (2006a). On the
state agreement problem for multiple unicycles. In
American Control Conference, 2006, page 6 pp.
Dimarogonas, D. and Kyriakopoulos, K. (2006b). On the
state agreement problem for multiple unicycles with
varying communication links. In Decision and Con-
trol, 2006 45th IEEE Conference on, pages 4283 –
4288.
Dimarogonas, D. and Kyriakopoulos, K. (2007). Connec-
tivity preserving state agreement for multiple unicy-
cles. In American Control Conference, 2007. ACC
’07, pages 1179 –1184.
Dong, W. and Farrell, J. (2008). Cooperative control of mul-
tiple nonholonomic mobile agents. Automatic Con-
trol, IEEE Transactions on, 53(6):1434 –1448.
D’Orsogna, M. R., Chuang, Y.-L., Bertozzi, A. L., and
Chayes, L. (2006). Self-propelled particles with soft-
core interactions: patterns, stability, and collapse.
Physical Review Letters.
Helbing, D., Farkas, I., and Vicsek, T. (2000). Simulating
dynamical features of escape panic. Nature, 407:487–
490.
Levine, H., Rappel, W.-J., and Cohen, I. (2001). Self-
organization in systems of self-propelled particles.
Phys, Rev. E, 63:017101.
Mogilner, A. and Edelstein-Keshet, L. (1999). A non-local
model for a swarm. J. Math. Biology, 38:534–570.
Moshtagh, N. and Jadbabaie, A. (2007). Distributed
geodesic control laws for flocking of nonholo-
nomic agents. IEEE Trans. on Automatic Control,
52(4):681–686.
Olfati-Saber, R. (2002). Near-Identity diffeomorphisms
and exponential ε-tracking and ε-stabilization of first-
order nonholonomic SE(2) vehicles. Proc. of the 2002
American Control Conference, 6:4690–4695.
Olfati-Saber, R. (2006). Flocking for Multi-Agent Dynamic
Systems: Algorithms and Theory. IEEE Trans. on Au-
tomatic Control, 51(3):401–420.
Parrish, J. K., Viscido, S. V., and Grunbaum, D. (2002).
Self-organized fish schools: an examination of emer-
gent properties. Biol. Bull., 202:296–305.
Partridge, B. L. (1982). The structure and function of fish
schools. Scientific American, 246(6):114–123.
Potss, W. K. (1984). The chorus-line hypothesis of maneu-
ver in avian flocks. Nature, 309:344–345.
Regmi, A., Sandoval, R., Byrne, R., Tanner, H., and Abdal-
lah, C. (2005). Experimental implementation of flock-
ing algorithms in wheeled mobile robots. In American
Control Conference, 2005. Proceedings of the 2005,
pages 4917 – 4922 vol. 7.
Reynolds, C. W. (1987). Flocks, herds, and schools: a dis-
tributed behavioral model. Computer Graphics (ACM
SIGGRAPH ’87 Conference Proceedings), 21(4):25–
34.
Shaw, E. (1975). Fish in schools. Natural History,
84(8):40–45.
Shimoyama, N., Sugawara, K., Mizuguchi, T., Hayakawa,
Y., and Sano, M. (1996). Collective motion in a
system of motile elements. Physical Review Letters,
76(20):3870–3873.
Tanner, H., Jadbabaie, A., and Pappas, G. (2005). Flock-
ing in teams of nonholonomic agents. In Kumar,
V., Leonard, N., and Morse, A., editors, Cooperative
Control, volume 309 of Lecture Notes in Control and
Information Sciences, pages 458–460. Springer Berlin
/ Heidelberg.
Toner, J. and Tu, Y. (1998). Flocks, herds, and schools:
A quantitative theory of flocking. Physical Review E,
58(4):4828–4858.
Topaz, C. M. and Bertozzi, A. L. (2004). Swarming patterns
in a two-dimensional kinematic model for biological
groups. SIAM J. Appl. Math.
Vicsek, T., Cziro
´
ok, A., Ben-Jacob, E., Cohen, I., and
Shochet, O. (1995). Novel type of phase transition in
a system of self-deriven particles. Phys. Rev. Letters,
75(6):1226–1229.
FlockingforNetworksofMobileRobotswithNonlinearDynamics
359