SAMPLING AND UPDATING HIGHER ORDER BELIEFS
IN DECISION-THEORETIC BARGAINING WITH FINITE
INTERACTIVE EPISTEMOLOGIES
Paul Varkey and Piotr Gmytrasiewicz
Department of Computer Science, University of Illinois at Chicago, 851 S. Morgan St., Chicago, U.S.A.
Keywords:
Bilateral bargaining, Decision theory, Interactive epistemology, Higher order beliefs, Belief sampling.
Abstract:
In this paper we study the sequential strategic interactive setting of bilateral, two-stage, seller-offers bargain-
ing under uncertainty. We model the epistemology of the problem in a finite interactive decision-theoretic
framework and solve it for three types of agents of successively increasing (epistemological) sophistication
(i.e. capacity to represent and reason with higher orders of beliefs). We relax typical common knowledge
assumptions, which, if made, would be sufficient to imply the existence of a, possibly unique, game-theoretic
equilibrium solution. We observe and characterize a systematic monotonic relationship between an agent’s
beliefs and optimal behavior under a particular moment-based ordering of its beliefs. Based on this character-
ization, we present the spread-accumulate technique of sampling an agent’s higher order belief by generating
“evenly dispersed” beliefs for which we (pre)compute offline solutions. Higher order prior belief identifica-
tion is then approximated to arbitrary precision by identifying a (previously solved) belief “closest” to the true
belief. These methods immediately suggest a mechanism for achieving a balance between efficiency and the
quality of the approximation – either by generating a large number of offline solutions or by allowing the agent
to search online for a “closer” belief in the vicinity of best current solution.
1 INTRODUCTION
The central challenge that arises in the epistemolog-
ical deliberations in strategic multi agent interactions
under uncertainty, is representing and reasoning with
the infinite interactive epistemology – first referred to
in game-theoretic literature as “the infinite regress in
reciprocal expectations” (Harsanyi, 1968).
Beginning with Harsanyi’s seminal work on
Games under Incomplete Information (Harsanyi,
1968), there is a long tradition of work and literature
that has attempted to combine the game-theoretic no-
tion of an equilibrium solution (Nash, 1950),(Nash,
1951) with a formal (probabilistic) calculus for rep-
resenting and reasoning with the players’ (individual,
mutual or common) knowledge or, lack thereof. The
solution concepts that have been proposed through-
out the history of this research effort involve, (see
first (Selten, 1975), then esp. (Fudenberg and Levine,
1981) and (Kreps and Wilson, 1982)), the proposal of
a profile of strategies and contingent beliefs for each
agent such that, given its beliefs, no agent has the in-
centive to deviate unilaterally. Further, the agents’ be-
liefs about the objects of uncertainty (for e.g. the path
of play, incl. esp. the previous choices of the other
agents) have to be consistent with (i.e plausible) with
respect to the joint profile of strategies.
No attempt will be made here to survey the field.
It suffices to simply point out that usefulness (or, ap-
plicability) of game-theoretic solution concepts as a
control paradigm in strategic multi agent interactions
is unclear, regardless of their mathematical and ab-
stract elegance and, oftentimes, powerful explanatory
power. This is primarily due to the fact that there
may be a multiplicity of equilibria for a particular
game; although, there is a vast literature (see, for
e.g., (Kreps, 1985), (Banks and Sobel, 1987), (Cho,
1987) and (Cho and Kreps, 1987)) discussing how
one may refine the set of equilibria and select among
them. Game-theoretic solution concepts have also
been challenged on the basis of the fact that the com-
mon knowledge prerequisite (Aumann and Branden-
burger, 1995) required to arrive at an equilibrium so-
lutions may be unattainable.
Increasingly, (Bayesian) decision-theoretic and
utility-theoretic approaches are becoming the domi-
nant and normative paradigm for reasoning and de-
cision making in settings under uncertainty. Recent
114
Varkey P. and Gmytrasiewicz P..
SAMPLING AND UPDATING HIGHER ORDER BELIEFS IN DECISION-THEORETIC BARGAINING WITH FINITE INTERACTIVE EPISTEMOLOGIES.
DOI: 10.5220/0003176901140123
In Proceedings of the 3rd International Conference on Agents and Artificial Intelligence (ICAART-2011), pages 114-123
ISBN: 978-989-8425-41-6
Copyright
c
 2011 SCITEPRESS (Science and Technology Publications, Lda.)

promising work extends this paradigm to interactive
(i.e. multi agent) settings (Gmytrasiewicz and Doshi,
2005), (Doshi and Gmytrasiewicz, 2005). In these
models, the recursive modeling of other agents’ be-
liefs and reasoning is made explicit in a framework
called the I-POMDP that extends classical POMDPs.
Computable (i.e. finitely nested) instances of these
models simply stop the recursive reflection after fi-
nite levels, allowing agents to make the best-possible
decision with the information they chose to repre-
sent. In essence, they are (expected utility maximiz-
ing) decision-theoretic models that represent and rea-
son with finite levels of the interactive belief hierar-
chy and make no (common knowledge) assumptions
regarding the levels that are not modeled.
This finite interactive decision theoretic model is
the assumed modeling framework throughout the cur-
rent work, where we study a particular interactive se-
quential game – namely, two-stage seller-offers bar-
gaining under incomplete information (Samuelson,
1984). It is known that this game has a unique Perfect
Bayesian Equilibrium (Sobel and Takahashi, 1983), if
it is asummed that the seller’s belief about the buyer’s
valuation is commonly known.
In this work, we do not make the assumption that
the seller’s (first-order) belief is commonly known.
Instead, we cast the problem in the finite interactive
decision theoretic framework for which we derive op-
timal strategies for three types of agents of succes-
sively increasing epistemological sophistication.
Our first main contribution is the observation of a
systematic regular (monotonic) relationship between
the epistemology of the problem and the agents’ op-
timal behavior. Secondly, this regularity is exploited
to devisea belief generation scheme that generates be-
liefs that are “evenly dispersed” across an entire space
of beliefs – equivalent to sampling the higher order
belief in “evenly dispersed” locations. And, thirdly,
solutions to these sample beliefs are precomputed of-
fline for later use in the online stage – which consists
of a binary search through the space of solved beliefs
to identify the closest sample belief in order to more
accurately approximately predict future behavior of
the opponent.
In the next section, we describe the model(s) used
throughout this paper and introduce necessary nota-
tions. In the following three sections, we describe, re-
spectively, the deliberative reasoning process for each
of the three strategy levels. Our main contributions
with respect to (higher order) belief sampling, identi-
fication and updating are presented in the context of
the discussion about the most sophisticated agent type
studies in this paper – the L3-Buyer (Section 5). In the
final section, we summarize our contributions, state
ongoing work and discuss relevant open questions.
2 PRELIMINARIES
Throughout this paper, it is assumed that the seller’s
valuation c = 0 and that the buyer’s valuation v is such
that 0 ≤ v ≤ 1. These are assumed to be commonly
known; the exact value of v is the buyer’s private in-
formation. The seller’s belief about the buyer’s val-
uation has the distribution F(v) = v;0 ≤ v ≤ 1. We
assume also that trade is feasible, i.e. that c ≤ v. The
mechanism is simple – the seller makes a first offer
x
1
which the buyer may chose to accept; if the buyer
rejects it, the seller makes a second and final offer x
2
.
The buyer strategic decision consists of choosing a
decision boundary d(x
1
) – it accepts the first offer x
1
if v ≥ d(x
1
).
If agreement is arrived at on the first day, the pay-
offs are x
1
and v − x
1
to the seller and buyer, respec-
tively. If agreement is arrivedat on the second day, the
payoffs are δ·x
2
and δ·(v−x
2
), respectively. Else, the
payoffs are 0 to either player. A discount factor, δ, is
applied to the payoffs on the second day.
Agents may form other relevant beliefs and
higher-order beliefs; for e.g. the seller may form a be-
lief about the buyer’s valuation, the buyer may form
a second-order belief about the seller’s first-order be-
lief about its (i.e. the buyer’s) valuation, etc. None of
these beliefs are assumed to be commonly known.
2.1 Notations
The following notation will be used throughout.
B
X
(p). Belief maintained by agent X (either seller
S or buyer B) about p, where p is the object of the
agent’s belief and may be a ground proposition or an-
other agent’s belief about something (this will be clear
from the context).
U(s). A uniform belief supported over a space s,
where s may be a (finite or countable) set of ground
propositions or a set of beliefs.
E[v]. Expected value of random variable v.
p
Accept
(x). The probability that offer x is accepted.
p
Reject
(x). The probability that offer x is rejected
(equal to 1− p
Accept
(x)).
π
1
(·). The expected utility function for the entire
(2-stage) sequential bargaining game. We denote
argmaxπ
1
(·) by Π
1
(·).
π
2
(·). The expected utility function for the last (i.e.
second) stage of the bargaining game. We denote
SAMPLING AND UPDATING HIGHER ORDER BELIEFS IN DECISION-THEORETIC BARGAINING WITH FINITE
INTERACTIVE EPISTEMOLOGIES
115

argmaxπ
2
(·) by Π
2
(·). The influence of an agent’s
belief on its objectivefunction is indicated by append-
ing the belief as a superscript to the expected utility
function as well as to the probabilities of an offer be-
ing accepted or rejected.
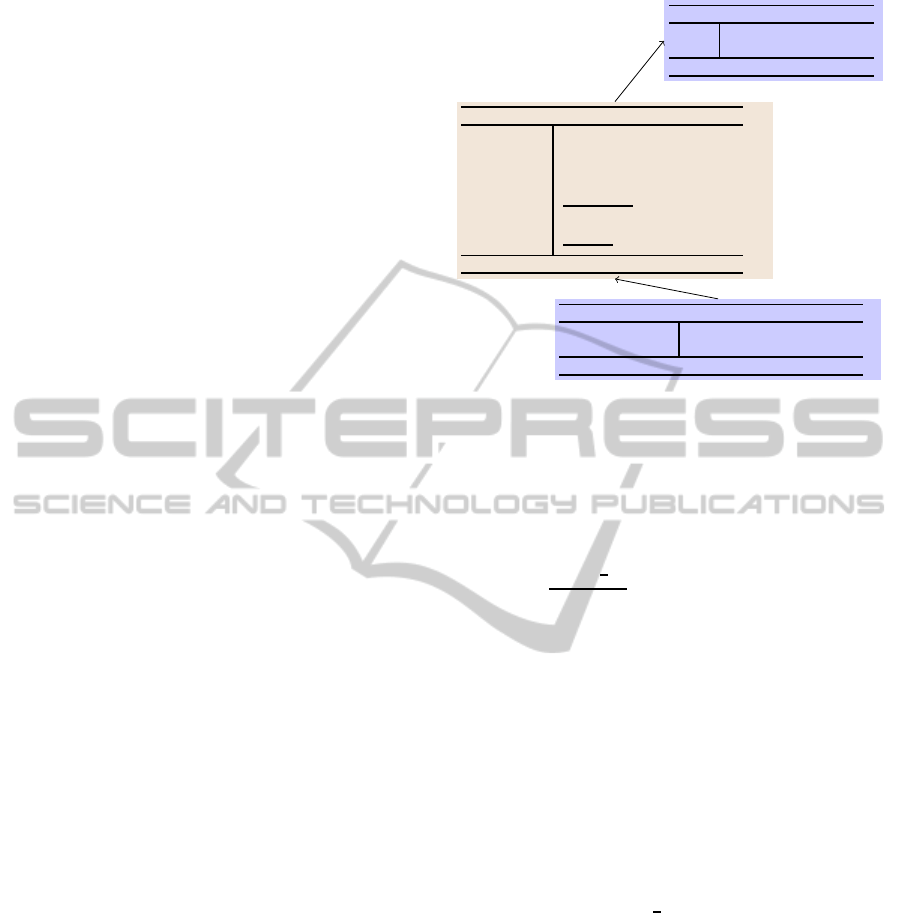
2.2 The Epistemic Setup
Using the notations introduced above, we now de-
fine the three types of successively more sophisticated
agents that are studied in this paper along with the in-
teractive epistemology that arises due to interactions
between these agents. Please see Figure 1 for a graph-
ical illustration of the same.
L1-Buyer believes that the seller’s first offer x
1
is
uniformly selected from (0,1) and that its sec-
ond offer is uniformly distributed between 0 (the
lowest possible) and the first offer, i.e. B
B
(x
2
) ∼
U(0,x
1
); in other words, that the seller’s second
offer is some arbitrary amount lesser than the first.
L2-Seller believes that the buyer’s belief about x
2
given x
1
is that it is supported on (0,x
1
) – al-
though, the seller does not “know” that this belief
is uniformly distributed. Therefore, it maintains a
higher (second) order belief that is supported on
some subset of all possible beliefs about x
2
given
x
1
that are supported on (0, x
1
), i.e. B
S
(B
B
(x
2
)) ∼
U(∆(0,x
1
)). The seller can express this higher-
order belief over a space of beliefs as a lower or-
der belief about the buyer’s expectation. Here we
say, for example, that the seller’s belief about the
buyer’s expectation of x
2
given x
1
– B
S
(E
B
[x
2
|x
1
])
– is uniformly distributed on (0, x
1
). Note that the
L2-Seller’s belief about the buyer’s type is char-
acterized here by its (second order) belief about
the buyer’s first order belief about the second of-
fer, or, equivalently, by its belief about the buyer’s
conditional expectation.
L3-Buyer The buyer believes that the seller’s belief
about E
B
[x
2
|x
1
] is supported on (0,x
1
) – although,
the buyer does not “know” that this belief is uni-
formly distributed; in other words, the buyer does
not “know” that the seller is uniformly uncertain
about the buyer’s belief about x
2
given x
1
. There-
fore, this buyer maintains a higher order belief
that is supported on some subset of all possible be-
liefs that the seller may maintain about E
B
[x
2
|x
1
].
3 L1-BUYER
The L1-Buyer accepts the first offer x
1
if the imem-
diate profit is not lesser than the expected profit from
about ∼ s.t.,∈ etc.
B
B
(x
1
) U(0, 1) ∈ ∆(0,1)
B
B
(x
2
) U(0, x
1
) ∈ ∆(0,x
1
)
L1-Buyer
about ∼ s.t.,∈ etc.
B
S
(v) F(v) = v
B
S
B
B
(x
1
) P
1
(∆(0,1)) ∈ ∆(∆(0,1))
B
S
B
B
(x
2
) P
2
(∆(0,x
1
)) ∈ ∆(∆(0,x
1
))
B
S
(E
B
[x
2
|x
1
]) U(0,x
1
) = px
1
p ∼ U(0,1]
B
S
(d)
x
1
−δ(U(0,x
1
))
1−δ
l
x
1
−δ(px
1
)
1−δ
p ∼ U(0,1]
L2-Seller
about ∼ s.t.,∈ etc.
B
B
B
S
(v) F(v) = v
B
B
(B
S
(E
B
[x
2
|x
1
])) P
3
(∆(0,x
1
)) ∈ ∆(∆(0,x
1
))
L3-Buyer
Figure 1: An interactive epistemology for bilateral bargain-
ing.
the next turn, i.e. if
v− x
1
≥ δ(v− E[x
2
|x
1
])
⇒ v− x
1
≥ δ(v− x
1
/2)
i.e. if
v ≥
x
1
− δ
1
2
x
1
1− δ
=: d, the decision cutoff
4 L2-SELLER
Note that the L1-Buyer believes that the second of-
fer x
2
is selected from some distribution in ∆(0,x
1
)
– namely, the space of all distributions supported on
(0,x
1
). Therefore, given x
1
, it can calculate the ex-
pected value of the second offer E
B
[x
2
|x
1
] – which is
all it needs to compute the optimal decison boundary.
For e.g., if the L1-Buyer believes that x
2
∼ U(0, x
1
)
(as is actually the case as shown in the previous sec-
tion), then E
B
[x
2
|x
1
] =
1
2
· x
1
. In general, E
B
[x
2
|x
1
]
has the form p · x
1
(for 0 ≤ p ≤ 1). Therefore, from
the L2-Seller’s perspective, only B
S
(E
B
[x
2
|x
1
]) – i.e.
its beliefs about E
B
[x
2
|x
1
] – matter when it reasons
about the buyer’s reasoning process following the re-
jection of the first offer. In the epistemics considered
here (see Figure 1), the seller believesthat E
B
[x
2
|x
1
] ∼
U(0,x
1
) (or, E
B
[x
2
|x
1
] = p· x
1
where p ∼ (0, 1]). The
seller’s best-response consists of the computation of
x
∗
1
such that
x
∗
1
∈argmax
x
1
π
B
S
(E
B
[x
2
|x
1
])
1
(x
1
)
= argmax
x
1
π
U(0,x
1
)
1
(x
1
)
ICAART 2011 - 3rd International Conference on Agents and Artificial Intelligence
116

= argmax
x
1

p
U(0,x
1
)
Accept
(x
1
) · x
1
+ δ· p
U(0,x
1
)
Reject
(x
1
) · Π
U(0,x
1
)
2
(x
1
)

The influence of the seller’s belief about E
B
[x
2
|x
1
] on
the values of the obective function at each stage and
on the probabilities of acceptance is indicated by in-
cluding the belief as the superscript of such values.
4.1 Uniform Belief with Finite Support
We now focus our attention on a specific epistemic
setup to fix intuition. Assume that B
S
(E
B
[x
2
|x
1
]) has
a distribution U
3
s.t.:
B
S
(E
B
[x
2
|x
1
]) ∼ U
3
∼ U

x
1
4
,
x
1
2
,
3x
1
4

The purpose of this setup is two-fold – first, it may
be seen as a simplified approximate version of the
seller’s actual belief and, second, it may also be
thought of as a means of gaining useful insight into
the epistemic deliberative and computational chal-
lenges inherent in the original problem.
Denote the corresponding values of the buyer’s
decision boundary d as d
1
, d
2
and d
3
, where
d
1
=
x
1
− δ
1
4
x
1
1− δ
, d
2
=
x
1
− δ
1
2
x
1
1− δ
& d
3
=
x
1
− δ
3
4
x
1
1− δ
If a particular offer x
1
is rejected, the resultant
posterior density from the seller’s belief update is a
weighted sum of three densities, represented pictori-
ally as:
d
1
f(d
1
)
1
3
·
+
1
d
1
d
2
f(d
2
)
1
3
·
+
1
d
2
d
3
f(d
3
)
1
3
·
=
1
d
3
d
f(d)
1
3
1
d
1
+
1
3
1
d
2
+
1
3
1
d
3
1
3
1
d
2
+
1
3
1
d
3
1
3
1
d
3
The probability that x
1
will be accepted can be ex-
pressed as:
p
U
3
Accept
(x
1
) =
1
3

F(1) − F(d
1
)
F(1)

+
1
3

F(1) − F(d
2
)
F(1)

+
1
3

F(1) − F(d
3
)
F(1)

=
1
3
(1− d
1
) +
1
3
(1− d
2
) +
1
3
(1− d
3
)
Now, the the seller assigns the following probabil-
ity to the buyer accepting the second offer:
p
U
3
Accept
(x
2
) =



























1
3
F(d
1
)−F(x
2
)
F(d
1
)
+
1
3
F(d
2
)−F(x
2
)
F(d
2
)
+
1
3
F(d
3
)−F(x
2
)
F(d
3
)
if x
2
≤ d
1
1
3
F(d
2
)−F(x
2
)
F(d
2
)
+
1
3
F(d
3
)−F(x
2
)
F(d
3
)
if d
1
≤ x
2
≤ d
2
1
3
F(d
3
)−F(x
2
)
F(d
3
)
if d
2
≤ x
2
≤ d
3
Accordingly, the seller’s second stage objective func-
tion (i.e. expected profit from offering some x
2
after
x
1
has been rejected) becomes:
π
2
(x
2
) =



























1
3
F(d
1
)−F(x
2
)
F(d
1
)
x
2
+
1
3
F(d
2
)−F(x
2
)
F(d
2
)
x
2
+
1
3
F(d
3
)−F(x
2
)
F(d
3
)
x
2
if x
2
≤ d
1
1
3
F(d
2
)−F(x
2
)
F(d
2
)
x
2
+
1
3
F(d
3
)−F(x
2
)
F(d
3
)
x
2
if d
1
≤ x
2
≤ d
2
1
3
F(d
3
)−F(x
2
)
F(d
3
)
x
2
if d
2
≤ x
2
≤ d
3
Let X
2
(x
1
) = argmax
x
2
π
2
(x
2
)
and Π
2
(x
1
) = max
x
2
π
2
(x
2
)
respectively.
We first obtain both of these as functions of x
1
from the piecewise first-order conditions for π
2
(x
2
).
Then, we express the seller’s main (first stage) objec-
tive function as:
π
1
(x
1
) =

1
3
(1−d
1
) +
1
3
(1−d
2
) +
1
3
(1−d
3
)

· x
1
+ δ·

1
3
d
1
+
1
3
d
2
+
1
3
d
3

· Π
2
(x
1
)
The first-order conditions for π
1
(x
1
) provide us
the seller’s optimal first offer X
1
as 0.3831693366
(from which we can easily compute the the optimal
second offer X
2
and the expected optimal profit Π
1
).
The algorithm for the general case (for evenly
distributed uniform discretized beliefs of finite
support) is provided by Procedure X1X2Pi1.
SAMPLING AND UPDATING HIGHER ORDER BELIEFS IN DECISION-THEORETIC BARGAINING WITH FINITE
INTERACTIVE EPISTEMOLOGIES
117

Procedure: X1X2Pi1(N,δ,p).
Input: N ← the number of samples, δ ← the
discount factor and p ← an array (of
size N) of probabilities
Output: X
1
← argmax
x
1
π
1
(x
1
),
X
2
(X
1
) ← X
2
(x
1
= X
1
) and
Π
1
(X
1
) ← π
1
(x
1
= X
1
)
// Given the number of samples, the
discount factor and a prior belief
sampling, returns the seller’s
optimal offer schedule and
expected optimal profit for the
case where
B
S
(v) := F(v) = v
begin
// D ← decision cutoffs
D[0] ← 0
for i from 1 to N − 1 do
D[i] ←
x
1
−δ(
N−i
N
)x
1
1−δ
// C π
2
← piecewise constrain
intervals
Cπ
2
[i] ← D[i− 1] < x
2
and x
2
≤ D[i]
// π
2
← final stage piecewise
objective function
π
2
[i] ←
N−1
∑
j=i
p[N − j]
D[ j] − x
2
D[ j]
x
2
//
∂π
2
∂x
2
← piecewise partial
derivative of π
2
w.r.t x
2
∂π
2
∂x
2
[i] =
∂π
2
[i]
∂x
2
end
// Initializations
X
2
← 0; Π
2
← 0
// Compute X
2
(x
1
) ← argmax
x
2
π
2
(x
2
) and
Π
2
(x
1
) ← max
x
2
π
2
(x
2
)
for i from 1 to N − 1 do
x
2
[i] ←
solve

∂π
2
∂x
2
[i],x
2

assuming Cπ
2
[i]
Let x
1
> 0 and x
2
← x
2
[i]
if Cπ
2
[i] and π
2
[i] > Π
2
then
X
2
← x
2
Π
2
← π
2
[i](X
2
)
end
end
// π
1
← the main (first stage)
objective function
π
1
(x
1
) ←

N−1
∑
j=1
p[N − j](1− D[ j])

x
1
+ δ

N−1
∑
j=1
p[N − j]D[ j]

Π
2
X
1
← solve

∂π
1
(x
1
)
∂x
1
,x
1

return X
1
, X
2
(x
1
= X
1
), π
1
(x
1
= X
1
)
end
We now highlight a few insights gained:
1. The optimal offers and optimal expected profits
for the cases when each of the sample points con-
sidered here is the certain case (i.e. w.p. 1), is
shown in Table 1.
Table 1: Optimal offers and expected profits when seller
“knows” E
B
[x
2
|x
1
].
β
†
x
β,∗
1
= argmax
x
1
Π
β
1
(x
1
) Π
β
1

x
β,∗
1

x
1
4
0.3453858608 0.1726929304
x
1
2
0.3874092010 0.1937046005
3x
1
4
0.4581245526 0.2290622763
†
β denotes B
S
(E
B
[x
2
|x
1
])
From this table, we notice, in particular, that
x
x
1
2
,∗
1
6= x
U
3
,∗
1
(though E[U
3
] =
x
1
2
), i.e. that
x
x
1
2
,∗
1
= 0.3874092010
6=
x
U
3
,∗
1
= 0.3831693366
though they are “very close”. This indicates at
least that, though E[U(0, x
1
)] =
x
1
2
,it is not neces-
sarily the case that
x
U(0,x
1
),∗
1
= x
x
1
2
,∗
1
In other words, the solution to an optimization
problem parametrized by a random variable may,
at best, only be approximated by the solution to
the related optimization problem parametrized by
the expected value of the parameter.
Table 2: Optimal offers and expected profits for uniform
discrete seller beliefs.
N x
U
N
,∗
1
= argmax
x
1
Π
U
N
1
(x
1
) Π
U
N
1

x
U
N
,∗
1

5 0.3822887563 0.1911443782
10 0.3805058597 0.1902529299
20 0.3796076053 0.1898038026
50 0.3790678491 0.1895339246
100 0.3788879236 0.1894439618
200 0.3787979719 0.1893989860
400 0.3787529981 0.1893764991
2. The solutions for evenly distributed uniform dis-
cretized beliefs of varying supports is collected in
Table 2. As we increase the support of the seller’s
belief (i.e. as N grows), we observe a Cauchy-
like behavior in the corresponding optimal (first)
offers. In ongoing work, we are attempting to es-
tablish whether these values do indeed converge
(as they seem to) and whether they converge to
x
U(0,x
1
),∗
1
(as hoped for).
ICAART 2011 - 3rd International Conference on Agents and Artificial Intelligence
118

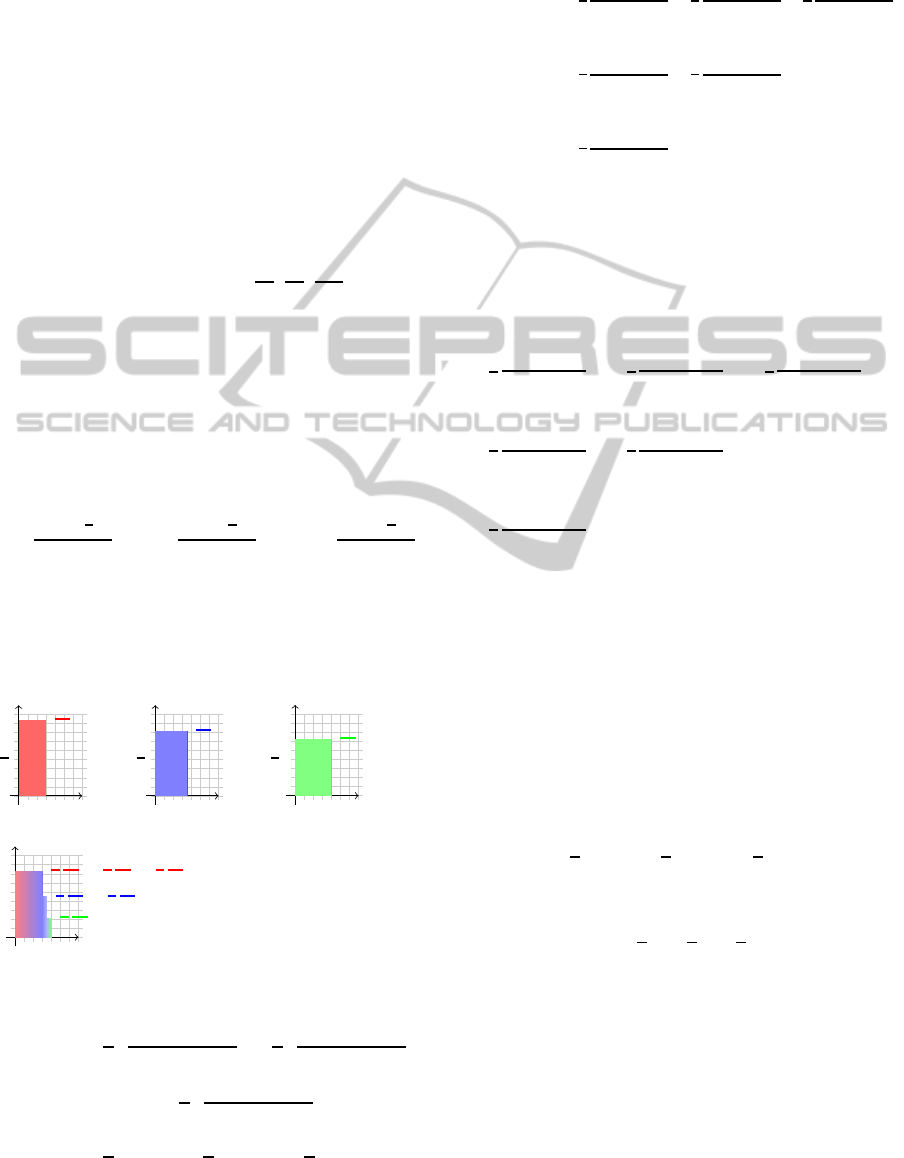
Beliefs, B
p
Objective
Functions, D
p,π
EXPECTATION
(INTEGRATION)
∈(0,1]
∈(0,1]
∈(0,1]
∈(0,1]
∈(0,1]
Optimal
Offers, X
∗
p,π
ARGMAX
Figure 2: The mapping from beliefs to objective functions
to optimal actions.
5 L3-BUYER
The L3-type buyer’s best response, i.e. either to reject
or accept the first offer x
1
, consists of computing the
optimal decision boundary d
∗
.
From the L3-Buyer’s perspective, its belief about
the seller’s belief about E
B
[x
2
|x
1
] (or, equivalently
its belief about the seller’s belief about p) – namely,
B
B
B
S
(E
B
[x
2
|x
1
]) (or, B
B
B
S
(p)) – constitutes the cru-
cial epistemic component that influences the compu-
tation of the optimal decision boundary.
In the simplest case, the L3-Buyer “knows” B
S
(p)
with certainty. In this case, it can solve the seller’s
optimization problem (for e.g., just like the seller
does, through sampling) to form expectations about
x
2
which, in turn, it uses to compute d
∗
.
In the general case, the buyer needs a method
whereby it can use the seller’s first offer as an infor-
mative signal to update B
B
B
S
(p) – i.e. to compute
B
B
B
S
(p|x
1
). The buyer deems a particular seller be-
lief implausible if a seller with such a belief would
have never sent the recieved (i.e. actual) first offer.
This constitutes the central contribution of the current
work and is discussed in detail next.
5.1 Higher Order Belief Identification
and Refinement (Update)
Figure 2 represents the mapping from the seller’s be-
lief to the objective function to the optimal (first) off-
fer. The L3-Buyer is interested in the inverses of these
mappings in order to refine the support of its belief
about the seller’s belief.
The L2-Seller’s objective function is parametrized
by its belief about E
B
[x
2
|x
1
] – which it expresses as a
belief about p (recall that E
B
[x
2
|x
1
] = p · x
1
). It ob-
tains the appropriate form of the objective function
by computing its expected value, i.e. by integrating
over its belief about p (see Figure 2).
Let B
p
be the class of all possible beliefs about p.
The seller’s objective function π is characterized by
parameter p (and, henceforth, will be written as π
p
).
Let D
p,π
p
be the class of all objective functions gen-
erated by integrating π over p for all possible beliefs
about p (i.e., over all elements of B
p
). The seller ob-
tains the optimal (first) offer from the first-order con-
ditions for the objective function.
In general, it is true that there are an uncountable
number of functions that share the same argmax in a
given interval. But, for the buyer, the relevant ques-
tion is
Question 1. Is the mapping from the seller’s possible
objective functions, D
p,π
, to the optimal offers, X
∗
p,π
p
,
injective?
A related and important question is
Question 2. Is the mapping from the seller’s beliefs
to objective functions injective?
Note that the buyer’s update process consists of
contingent-factual reasoning which may involve in-
verting the two discussed mappings (Figure 2). Such
inversions necessitate that the maps be injective.
Unfortunately, these maps are not injective; an ob-
servationwhich can be established by a few examples.
So, then, how does the buyer update its belief?
It is in the context of this problem that we present
the main contribution of this paper. Our approach in-
volves looking at the buyer’s belief update problem
in the other (i.e. the forward) direction – i.e. from
the seller’ beliefs to its actions. Establishing that the
optimal offers (schedules) are monotonic w.r.t. some
suitable ordering of the seller’s beliefs would point
to a means of identifying the seller’s next offer (with
arbitrary precision) by searching for a close-enough
belief that would explain the seller’s first offer. We
now proceed to expound this idea in depth.
5.2 (µ,σ)-Ordered D.F.s
Consider the seller’s objective function π
p
: [0, 1] →
R
+
. π
p
is continuous and differentiable in [0, 1] and
attains its maximum value at the only saddle-point in
the same interval. π
p
is parametrized by a random
variable p (where 0 ≤ p ≤ 1). If the distribution F of
p is known, one can calculate the expectation of the
function π
p
:
E
F
(π
p
) =
Z
1
0
π
p
dF
Since the buyer does not, in general, know F, we as-
sume that the distribution function of p comes from a
family of distribution functions F
p
. Here, we define a
particular ordering for classes of distributions.
Order
(µ,σ)
(F ). Given a class of distribution functions
F , Order
(µ,σ)
(F ) is a (total) ordering of F based on
SAMPLING AND UPDATING HIGHER ORDER BELIEFS IN DECISION-THEORETIC BARGAINING WITH FINITE
INTERACTIVE EPISTEMOLOGIES
119

the expectation (i.e. mean value) of the member dis-
tributions, where, if possible, ties are broken by fur-
ther (totally) ordering based on the variance of the
member distributions. In symbols,
F ≺
Order
(µ,σ)
(F )
G
if µ(F) < µ(G) or
µ(F) = µ(G) and σ(F) > σ(G)
∀ F,G ∈ F
Now consider a sequence of distribution functions
F
1
,F
2
,F
3
,... from F
p
that respects Order
(µ,σ)
(F
p
) in
addition to satisfying an additional technical require-
ment that the F
n
are “not too close”.
We obtain empirical evidence that indicates that,
under such an ordering, the distribution functions F
n
have a monotonic influence on the saddle-point of
E
F
n
(π
p
), i.e.:
argmax E
F
n
(π
p
) =
Z
1
0
π
p
dF
n
≤
argmax E
F
m
(π
p
) =
Z
1
0
π
p
dF
m
whenever 1 ≤ n < m.
This seems to be the case because of the fact that
p exerts a monotonic influence on argmax π
p
(see
Table 1). Clearly, this observation is specific to the
problem and the mechanism under consideration and
it is not immediate whether it is true in general. The
statement and proof of a general result of this type is
a subject of current work.
In any case, the empirically established monotonic
behavior observed in the current settings provides suf-
ficient grounds for the development of the higher or-
der belief identification method that is outlined in the
next subsection.
5.3 (µ,σ)-ordered Spread-Accumulate
Sample Generation Method for
Higher Order Belief Sampling
Based on the observations of the previous section,
the buyer can pre-compute the seller’s optimal first
offer for various seller belief settings
1
that are “ap-
propriately evenly dispersed” according to the (µ,σ)-
ordering. Then, when it recieves a particular first of-
fer from the seller, it can first find the nearest pre-
computed belief setting that explains this offer and,
1
For convenience, we only consider discrete beliefs
if necessary, search in the (µ,σ)-vicinity of this belief
for a “better explanation”.
First, we need a systematic method of sampling to
choose and solve for a set of beliefs that are “appro-
priately evenly dispersed” across the entire space of
possible beliefs (in the buyer’s support). At the least,
the method has to select a set of distributions with
mean values that range from one extreme end of the
support interval to the other. Further, for a particu-
lar mean, it has to select distributions with a range of
variances – from low to medium to high.
We have devised exactly such a method – and
we call it the spread-accumulate sample generation
method. It consists of the following steps:
1. Discretize the support of the seller’s belief (about
p) uniformly into N intervals. Here p ∈ (0, 1];
therefore, the discretized beliefs will be supported
on

1
N
,
2
N
,...,
N−1
N

.
2. Generate discrete distributions each of which has
a mean exactly equal to one of the support points
(for all values from

1
N

to

N−1
N

), for differ-
ent settings of the variance (from low to high).
Two distinct kinds of cases can be identified: Ex-
treme points (2 cases). The entire mass of the
distribution (= 1) is concentrated on one of the
extreme points of the supporing set. The variance
setting cannot be changed (i.e. decreased) any fur-
ther without shifting the mean. Interior points
((N− 3)(N− 1) cases). For a particular mean, we
first choose and solve for the discrete belief which
concentrates all its mass on the mean value. Then,
this being the key step of the spread-accumulate
method, we select distributions by alternatively
successively spreading out the probability mass
from the previous distributions to neighbouring
points and then accumulating some probability
mass from the interior points to the most extreme
points with positive mass. An example will illu-
minate: Let N = 7. Let the desired mean be
4
7
.
Then, the spread-accumulate method generates
discrete distributions on the support

1
7
,
2
7
,...,
6
7

in the following order (only probability masses
are specified for the points in the support in the
natural order):
0, 0, 0, 1, 0, 0
0, 0,
1
3
,
1
3
,
1
3
, 0
0, 0,
1
2
, 0
1
2
, 0
0,
1
4
,
1
4
, 0,
1
4
,
1
4
0,
1
2
, 0, 0, 0,
1
2
2
5
, 0, 0, 0, 0,
3
5
The buyer solves the seller’s optimization prob-
lem for each of the generated sample beliefs and
ICAART 2011 - 3rd International Conference on Agents and Artificial Intelligence
120

stores the corresponding optimal schedules (the first
and second offers) in 2D arrays. The whole pro-
cess – spread-accumulate sample generation and op-
timal schedule computation – is described in Proce-
dure L3BuyerOfflineX1X2Pi1. Row i corresponds to
beliefs with mean=
i
N
. The column entries corre-
spond to different settings of the variance – from low
(entry 1) to high (entry n− 1).
5.4 Online Computation of d
∗
The offline pre-computation of the seller’s optimal
schedule for various seller belief settings, described in
the previous section, enables the buyer to identify the
“closest” belief in the (µ,σ)-orderingto the seller’s ac-
tual belief (this is exactly the belief that is associated
with the optimal first offer closest to the seller’s ac-
tual first offer). In the offline step, the buyer stores re-
sults into the 2D array in the naturally available mono-
tonic ordering – this is exploited here to implement
the buyer’s closest-belief-identification procedure as
a binary search. The buyer can then also, optionally,
perform a refined search (through further sampling
and computation) in this vicinity to identify a “closer”
belief. Once the buyer finds a “close enough” solution
(to arbitrary precision), it uses the associated optimal
second offer to compute d
∗
. This process is formally
outlined in Procedure L3BuyerGetX1RetD*.
5.5 An Example
We consider the case of an L2Seller, Sam bargain-
ing with an L3Buyer, Bob. (We also assume that
δ = 0.6 throughout this example). Sam models the
buyer as an L1-type buyer (cf. Section ) and has the
following belief about the buyer’s expectation of the
second offer given the first: B
S
(E
B
[x
2
|x
1
]) = p · x
1
where p is supported on [2/5, 4/5] with respective
probabilites [2/3,1/3]. This may be interpreted as
Sam’s belief that Bob is twice as likely to expect a
huge decrease in the second offer, corresponding to
P
B
S
(E
B
[x
2
|x
1
])
(p = 2/5) = 2/3, than not. Sam’s prob-
lem may be solved to obtain the optimal offers as:
x1
∗
Sam
= 0.39 and x2
∗
Sam
= 0.32
Now, we consider Bob’s offline step. Say that Bob
chooses discretization paramater, N, to be 6. Bob’s
solution for all the 17 (= 2 + (N − 3)(N − 1)) sam-
pled belief points are recorded in Table 3 where
each entry (i, j) is a 2-tuple (X1[i, j],X2[i, j]), such
that X1[i, j] and X2[i, j] comprise the solution corre-
sponding to the belief sample with mean
i
N
and vari-
ance corresponding to the j
th
smallest for that par-
ticular mean value (generated according to spread-
accumulate sampling).
Procedure: L3BuyerOfflineX1X2Pi1(N,δ).
Input: N ← the number of discretization intervals
and δ ← the discount factor
Output: X
1
, X
2
and Π
1
← (N −1) × (N −1) 2D
arrays representing, respectively, the
optimal schedule and optimal expected
profit to the seller for different settings of
seller beliefs
// Procedure X1X2Pi1 will be invoked
throughout
begin
// a ← a size (N − 1) probability
vector
a ← {1,0,...,0}
(X
1
[1,1],X
2
[1,1],Pi
1
[1,1]) = X1X2Pi1(N,δ,a)
for m from 2 to N − 2 do
a ← {0,0,...,0}, a[m] = 1
(X
1
[m,1], X
2
[m,1], Pi
1
[m,1]) =
X1X2Pi1(N, δ,a)
a ← {0,0,...,0},
a[m−1] = a[m] = a[m+ 1] =
1
3
(X
1
[m,2], X
2
[m,2], Pi
1
[m,2]) =
X1X2Pi1(N, δ,a)
a ← {0,0,...,0}, a[m− 1] = a[m+ 1] =
1
2
(X
1
[m,3], X
2
[m,3], Pi
1
[m,3]) =
X1X2Pi1(N, δ,a)
c = min (m− 2,N − 2− m)
for n from 1 to c do
a ← {0,0,...,0}, a[m+ n+ 1] =
a[m+ n] = a[m− n] = a[m− n− 1] =
1
4
(X
1
[m,2n+ 2],X
2
[m,2n+
2],Pi
1
[m,2n+ 2]) = X1X2Pi1(N, δ,a)
a ← {0,0,...,0},
a[m+ n+1] = a[m−n− 1] =
1
2
(X
1
[m,2n+ 3],X
2
[m,2n+
3],Pi
1
[m,2n+ 3]) = X1X2Pi1(N, δ,a)
end
if m <
N
2
then
for l from 2m to N −1 do
a ← {0,0, ...,0}, a[1] =
m−l
1−l
and
a[l] = 1− a[1]
(X
1
[m,l], X
2
[m,l], Pi
1
[m,l]) =
X1X2Pi1(N, δ,a)
end
else
for l from 1 to 2m−N do
a ← {0,0, ...,0},
a[2m−N − l +1] =
m−N+l
2m−2N−l+2
and
a[N − 1] = 1− a[2m− N −l + 1]
(X
1
[m,2N − 2m+ l− 1],X
2
[m,2N −
2m+ l − 1], Pi
1
[m,2N − 2m+ l −
1]) = X1X2Pi1(N,δ, a)
end
end
end
a ← {0,0,...,1}
(X
1
[N − 1,1],X
2
[N − 1, 1],Pi
1
[N − 1,1]) =
X1X2Pi1(N, δ,a)
return X
1
, X
2
, Π
1
end
SAMPLING AND UPDATING HIGHER ORDER BELIEFS IN DECISION-THEORETIC BARGAINING WITH FINITE
INTERACTIVE EPISTEMOLOGIES
121

Table 3: Output of Procedure L3BuyerOfflineX1X2Pi1 for Bob.
i ↓ , j → 1 2 3 4 5
1 0.3354,0.3773 – – – –
2 0.3571,0.3571 0.3555,0.3518 0.3547,0.3492 0.3517,0.3391 0.3478,0.3260
3 0.3874,0.3389 0.3855,0.3327 0.3846,0.3296 0.3803,0.3155 0.3764,0.3025
4 0.4301,0.3225 0.4277,0.3148 0.4266,0.3111 0.4242,0.3030 0.4224,0.2970
5 0.4923,0.3076 – – – –
Procedure:L3BuyerGetX1RetD*(x1,N,X1,X2,δ).
Input: x1 ← the (L2-type) seller’s first offer, N ←
the dimension of the precomputed 2D arrays,
X1 and X2 and δ ← the discount factor
Output: s
∗
← the (L3-type) buyer’s decision
boundary
// The set of beliefs with the closest
mean value if first identified using
binary search; then, the belief with
the closest variance is identified
using linear search through this class
begin
l ← 1
u ← N − 1
for i from 1 to ceil(ln(N) + 1) do
if x1 ≥ X1

ceil

l+u
2

,1

then
l ← floor

l+u
2

else
u ← ceil

l+u
2

end
end
i
1
← l
i
2
← 1
ε ← |x2− X1[i
1
,i
2
]|
for i from 1 to N − 1 do
if |X1[u,i] − x
1
| ≤ ε then
i
1
← u
i
2
← i
ε ← |X1[u,i] − x
1
|
end
end
d
∗
←
x1−δX2[i
1
,i
2
]
1−δ
return d
∗
end
Procedure L3BuyerGetX1RetD*’s trace with respect
to Table 3 shows that, after three binary search
steps and five linear search steps, the “closest” pre-
computed first offer given the actual value of 0.39 is
0.3874, corresponding to X1[3,1]. The corresponding
best estimate of the second offer, X2[3,1], is 0.3389,
which is very close to the actual second offer, 0.32.
The cutoff that is computed is
x1− δ · X2[3,1]
1− δ
=
0.39− 0.6· 0.3389
1− 0.6
= 0.46665
while the optimal cutoff is
x1− δ · x2
1− δ
=
0.39− 0.6· 0.32
1− 0.6
= 0.495
Notice, importantly, that only a significantly small
fraction of buyers, those with valuations in the range
[0.46665,0.495], make the wrong decision to accept
the first offer. In particular, for e.g., in the assumed
commonly known epistemology analysed here, the
bueyrs are uniformly distributed in [0, 1], implying
that 97.165% of the buyers make the right decision.
6 CONTRIBUTIONS AND
ONGOING WORK
In the course of analyzing the L2-Seller (cf. Section
4), we graphically illustrated the step-function shape
of a (Bayesian) updated belief density for an agent
that maintains a discrete uniform prior belief and uses
the opponent’s signal as a screening device. In ongo-
ing work, we are working on a generalized belief up-
date method for computing posterior densities using
a screening signal for general (i.e. non-uniform) dis-
crete prior beliefs. In addition, we are investigating
whether the optimal strategies of the L2-Seller con-
verge when we increase the number of samples used
to represent its discrete uniform prior belief.
In Section 5, we analyzed the L3-Buyer and
presented the central contributions of this paper.
We made an important observation about the reg-
ular (monotonic) influence of a particular ordering,
namely, the (µ,σ)-ordering, of distribution functions
of a random variable on the (maximal) saddle-point of
an objective function that is paramatrized by that vari-
able. In this context, we presented a question that will
be the subject of future work: Does the observed reg-
ular (monotonic) influence occur because the random
variable itself exerts a similar monotonic influence?
A second question that is a foundational to extend-
ing these results is, In general, when do the (central)
moments suffice in completely characterizing the in-
fluence of the epistemology of the problem on optimal
behavior? And, when they do, how many (central)
moments suffice?
ICAART 2011 - 3rd International Conference on Agents and Artificial Intelligence
122

Next, we motivated and developed the spread-
accumulate (belief) sample generation method. This
method enables the generation of “evenly dispersed”
samples from the higher order belief space. These
samples are then pre-solved offline to facilitate on-
line binary-search for the “closest” belief instead of
doing exact belief update (which may be analyticaly
unachievable and numerically intractable). In this
manner, we are able to realize (approximate) higher-
order belief update. The monotonicity property of the
(µ,σ)-ordering is exploited to implement the binary
search through the space of (sampled and pre-solved)
beliefs to identify the closest representative.
We then proposed that this higher-order belief
update (or, approximate identification) scheme may
be seen as an online-refinement based realization of
bounded rationality. If the precomputed solutions are
not “close enough” (within some desired precision),
the agent can perform further online computations
and fine-grained search within the (µ, σ)-vicinity of
the current best solution. The agent can increase the
quality of its offline solutions during its down-time as
well as seek a better approximations online.
6.1 Conclusions
In conclusion, we have demonstrated the usefulness
and epistemological modeling power of the frame-
work of multi-agent decision-theoretic reasoning and
sequential planning with finite interactive epistemol-
gies (Gmytrasiewicz and Doshi, 2005) for the real-
world problem of bilateral bargaining. We focussed
on the problem of higher-order belief update in this
context and presented some regularity results that
connected beliefs (epistemology) and behavior (opti-
mal strategies). Based on this, we developed a novel
evenly-dispersed higher order belief sample genera-
tion scheme (the spread-accumulate method) for ap-
proximating higher-order belief identification in order
to (approximately) realize higher-order belief update.
Our methods are potentially generalizable to other
problem domains that involve strategic multiagent in-
teractions – all that needs to be done is to check
whether the epistemology-optimal behaviour regular-
ity phenomenon holds for a given problem. A com-
plete characterization of general epistemological and
strategic conditions under which this phenomenon
arises is crucial for advancing the finite epistemolog-
ical decision-theoretic framework and for completing
the theory of intelligent and autonomous behavior in
multiagent settings.
REFERENCES
Aumann, R. and Brandenburger, A. (1995). Epistemic
conditions for nash equilibrium. Econometrica,
63(5):1161–1180.
Banks, J. and Sobel, J. (1987). Equilibrium selection in
signaling games. Econometrica, 55(3):647–661.
Cho, I.-K. (1987). A refinement of sequential equilibrium.
Econometrica, 55(6):1367–1389.
Cho, I.-K. and Kreps, D. (1987). Signaling games and sta-
ble equilibria. The Quarterly Journal of Economics,
102(2):179–222.
Doshi, P. and Gmytrasiewicz, P. (2005). Approximating
state estimation in multiagent settings using particle
filters. In In Proceedings of the Fourth International
Joint Conference on Autonomous Agents and Multia-
gent Systems.
Fudenberg, D. and Levine, D. (1981). Perfect equilibria of
finite and infinite horizon games.
Gmytrasiewicz, P. and Doshi, P. (2005). A framework for
sequential planning in multi-agent settings. Journal of
Artificial Intelligence Research, 24:49–79.
Harsanyi, J. C. (1968). Games with incomplete informa-
tion played by ’bayesian’ players, i-iii. Management
Science, 14:pp. 159–182, 320–334, 486–502.
Kreps, D. (1985). Signaling games and stable equilibria.
Kreps, D. and Wilson, R. (1982). Sequential equilibria.
Econometrica, 50:863–894.
Nash, J. (1950). Equilibrium points in n-person games.
Proceedings of the National Academy of Sciences,
36(1):48–49.
Nash, J. (1951). Non-cooperative games. The Annals of
Mathematics, 54(2):286–295.
Samuelson, W. F. (1984). Bargaining under asymmetric in-
formation. Econometrica, 52(4).
Selten, R. (1975). Reexamination of the perfectness con-
cept for equilibrium points in extensive games. Inter-
national Journal of Game Theory, 4:25–55.
Sobel, J. and Takahashi, I. (1983). A multistage model of
bargaining. Review of Economic Studies, 50(3).
SAMPLING AND UPDATING HIGHER ORDER BELIEFS IN DECISION-THEORETIC BARGAINING WITH FINITE
INTERACTIVE EPISTEMOLOGIES
123