THE SIGNING OF A PROFESSIONAL ATHLETE
Reducing Uncertainty with a Weighted Mean Hemimetric for Φ − Fuzzy Subsets
Julio Rojas-Mora and Jaime Gil-Lafuente
Dpto. de Econom
´
ıa y Organizaci
´
on de Empresas, Universitat de Barcelona
Diagonal 690, 08034, Barcelona, Spain
Keywords:
Fuzzy sets, Distance, Human resources selection.
Abstract:
In this paper we present a tool to help reduce the uncertainty presented in the decision-making process associ-
ated to the selection and hiring of a professional athlete. A weighted mean hemimetric for Φ − fuzzy subsets
with trapezoidal fuzzy numbers (TrFN) as their elements, allows to compare candidates to the “ideal” player
that the technical body of a team believes should be hired.
1 INTRODUCTION
Uncertainty is present in all the decision-making pro-
cesses we face. In human resources selection, there
is a great deal of uncertainty. Employers check refer-
ences and apply a battery of tests to candidates, with
the hope of making an appropriate choice to fill the
vacancy.
In professional sports, the decision-making pro-
cess associated with the hiring of an athlete involves
facing a possible sporting and economic fiasco
1
, due
to strategic factors associated with the selected can-
didate and the magnitud of the contracts signed. A
wrong decision could disrupt a championship and the
future of a team. Therefore, a large number of vari-
ables from the different areas that can determine the
success of an athlete, must be analyzed: technical,
tactical, physical performance, medical, economic,
psychological, social or other. To make things more
complicated, selection criteria can be different be-
tween a coach that needs to fill a particular need, a
general manager or executive who is interested on in-
mediate impact, or an owner who would like to sign
someone who helps boost attendance(Young, 2008).
Win percentage, can be seen as a metric associated
with performance of sports teams(Borghesi, 2008).
In sports with a high production of statistics, the
marginal production associated with the recruitment
of a new team member can be easily studied. The
research line that develops statistical methods for as-
sessing the appropriateness of an athlete signing, has
1
14 english clubs entered administration and were effectively
insolvent”, as reported by (Sloane, 2006).
been deeply analized (Krautmann and Oppenheimer,
2002; Hendricks et al., 2003; Massey and Thaler,
2006). Nonetheless, it is difficult to allocate the pre-
cise fraction that a player contributes to the victory of
a team
2
.
In sports like football
3
, there are very few vari-
ables stochastical in nature. Most of the characteriza-
tion of a player is made through scouting reports, with
assesments that are filled with subjective information.
The theory of fuzzy subsets created by (Zadeh,
1965), is the tool that allows us to mathematically
model the uncertainty and seek solutions to the prob-
lems it presents. One of the issues explored is to de-
termine the best among a group of candidates, when
we are in the presence of uncertainty
4
.
The evaluation of candidates in the presence of
2
Win Shares, an statistical method for baseball found in (James
and Henzler, 2002), assigns 3 shares to each team win. Total win
shares for the team are distributed to the team members by an anal-
ysis of their individual performance, their performance in the con-
text of their home field and their performance relative to that of
their league. In each league, every year is different, but the amount
of games per season is constant over time. This allows to make
comparisons between athletes who played at times when there was
a preponderance of either the offensive or defensive. Also, compar-
isons between players of different field positions are possible.
3
Soccer.
4
As an example of this line of research, we can observe the
work of (Chen and Wang, 2001) and its application to the search
for the perfect home (Chen and Wang, 2007). The work developed
by (Yang et al., 2005) and its application in databases is also very
interesting. Even the International Olympic Committee has used
a method based on the theory of fuzzy subsets for the selection of
the venue of the 1st Summer Youth Olympic Games (IOC Panel of
Experts, 2007).
158
Rojas-Mora J. and Gil-Lafuente J. (2009).
THE SIGNING OF A PROFESSIONAL ATHLETE - Reducing Uncertainty with a Weighted Mean Hemimetric for Φ - Fuzzy Subsets.
In Proceedings of the 11th International Conference on Enterprise Information Systems - Artificial Intelligence and Decision Support Systems, pages
158-163
DOI: 10.5220/0001986101580163
Copyright
c
 SciTePress

uncertainty is based on the experience of the evalua-
tor, who has a key role in helping to reduce it. The
use of fuzzy subsets in the human resources selec-
tion process, since the seminal works of (Gil-Aluja,
1987; Gil-Aluja, 1996), has been a profoundly stud-
ied line of research (Cannavacciuolo et al., 1994; Gil-
Lafuente, 1999; Gil-Lafuente, 2000; Gil-Lafuente,
2001; Gil-Lafuente, 2005; Rojas-Mora and Gil-
Lafuente, 2008).
We follow on this research with a weighted mean
hemimetric for Φ − fuzzy sets, specially designed to
evaluate the case when the assessment of a candi-
date’s characteristic, modelled as a trapezoidal fuzzy
number, reaches that of an “ideal” candidate, but
doesn’t exceed it.
The reasoning behind this condition is simple. In
the process of selecting human resources, there are
situations where we only need to know how much
a candidate’s characteristics needs to the reach the
required level. By modeling with trapezoidal fuzzy
numbers we find that the assessment given to the can-
didate may overlap in whole or in part the level set
by the recruiter. Therefore, we will limit ourselves to
measure the distance from the candidate’s assessment
to the “ideal” level, in areas where he has not reached
it.
The rest of this paper is organized as follows; on
section 2 a brief definition of fuzzy numbers is car-
ried out. A hemimetric for trapezoidal fuzzy numbers
and a weighted mean hemimetric for Φ − fuzzy sets
is presented on section 3. An small example on how
the numerical calculations are carried out is shown on
section 4. Finally, section 5 comprises some conclu-
sions.
2 FUZZY SUBSETS AND FUZZY
NUMBERS
In situations of uncertainty, the theory of fuzzy sub-
sets can model assessments that, on a particular topic,
an expert gives out. These assessments take the form
of fuzzy subsets.
Definition 2.1. A fuzzy subset
˜
A is a set in which its
elements may not follow the law of excluded middle
that rules over boolean logic, i.e., their membership
function can be mapped as:
µ
˜
A
: X → [0, 1]. (1)
In general, a fuzzy subset
˜
A can be represented
by a set of pairs consistents of the elements x of the
universal set X and a grade of membership µ
˜
A
(x):
˜
A =
{
(x, µ
˜
A
(x)) | x ∈ X , µ
˜
A
(x) ∈ [0, 1]
}
. (2)
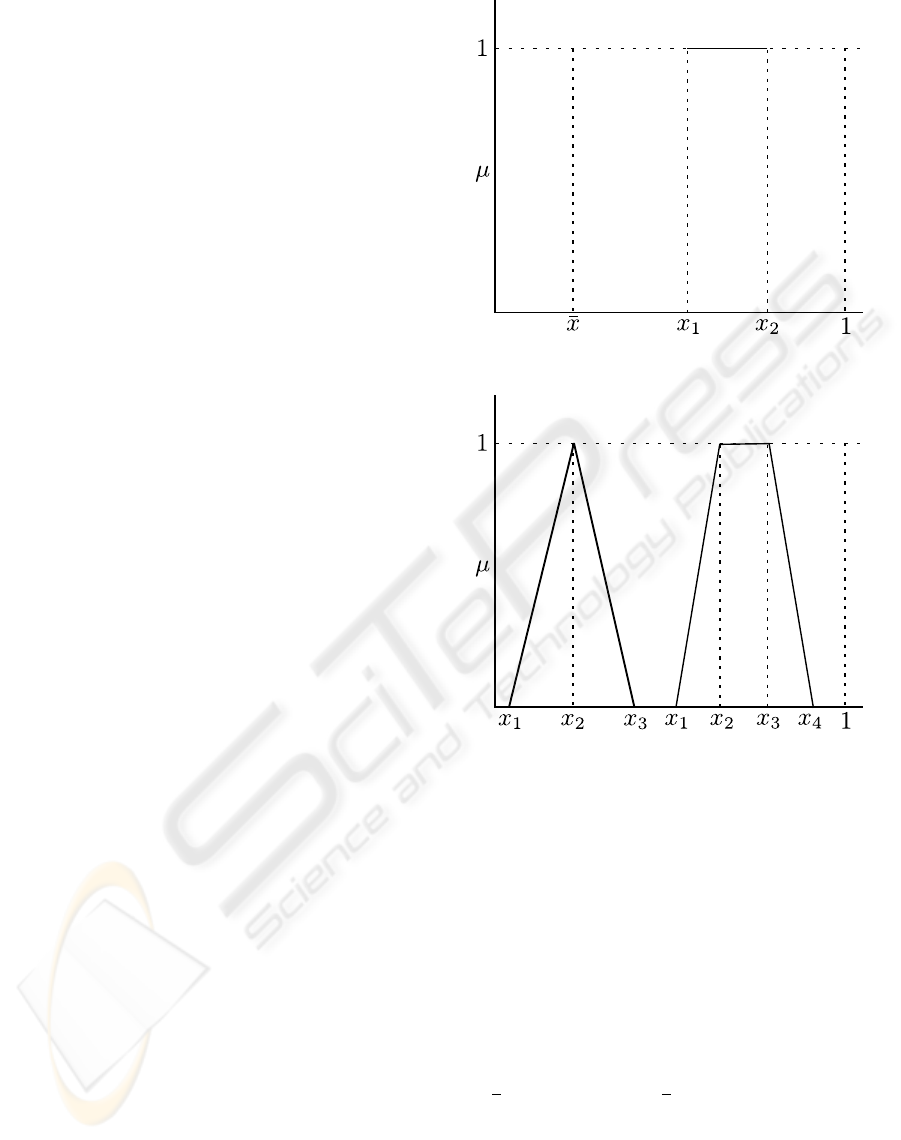
Figure 1: Fuzzy singleton and interval of confidence.
Figure 2: Triangular fuzzy number (TFN) and trapezoidal
fuzzy number (TrFN).
Definition 2.2. A fuzzy number
˜
M is a fuzzy subset
for which:
1. x ∈ R.
2. hgt(
˜
M) = 1, i.e., there is at least one element for
which µ
˜
M
(x) = 1.
3. λu + (1 − λv) ∈ M
α
∀u, v ∈ M
α
∧ α, λ ∈ [0, 1],
where M
α
is the α-cut for
˜
M. This is, the con-
vexity condition holds.
Remark. There is a fourth condition (Hanss, 2005)
which states that in a fuzzy number
˜
M there is exactly
one x ∈ R for which µ
˜
M
(x) = 1. However, as (Zim-
mermann, 2005, 57) explains, for computational sim-
plicity there is a tendency, that we will follow, to avoid
this condition, calling “fuzzy numbers” the fuzzy sub-
sets that meet the first three conditions. Moreover, in
fuzzy numbers used throughout this paper x ∈ [0, 1]
(see figures 1 and 2).
THE SIGNING OF A PROFESSIONAL ATHLETE - Reducing Uncertainty with a Weighted Mean Hemimetric for Y -
Fuzzy Subsets
159

In this work, assessments obtained from experts
take the form of fuzzy numbers. Entropy of these as-
sessments, namely the certainty the expert shows in
his opinion, is observed in the area covered by fuzzy
numbers. For the purposes of this study, we define
four kinds of fuzzy numbers according to their en-
tropy.
Definition 2.3. A fuzzy number whose support is a
single point ¯x is called a fuzzy singleton, and its mem-
bership function is:
µ
˜
M
(x) =
(
1 , if x = x
0 , else.
Definition 2.4. When there is not enough certainty to
give an assessment as a singleton, but it can be given
as an interval (x
1
, x
2
), we are defining an interval of
confidence with membership function:
µ
˜
M
(x) =
(
1 , if x
1
≤ x ≤ x
2
0 , else.
Definition 2.5. When there is a maximun of presump-
tion (Kaufmann and Gupta, 1985, 1) in x
2
, but the cer-
tainty linearly decreases to zero in x
1
and x
3
, we are
talking of a triangular fuzzy number (TFN) (x
1
, x
2
, x
3
)
with membership function:
µ
˜
M
(x) =





1 +
x
2
−x
x
2
−x
1
, if x
1
≤ x ≤ x
2
1 +
x−x
2
x
3
−x
2
, if x
2
< x ≤ x
3
0 , else.
Definition 2.6. When the maximum of presumption
covers the interval between x
2
and x
3
, and then lin-
early decreases to zero in x
1
and x
4
, we are defining a
trapezoidal fuzzy number (TrFN) (x
1
, x
2
, x
3
, x
4
) with
membership function:
µ
˜
M
(x) =









1 +
x
2
−x
x
2
−x
1
, if x
1
≤ x < x
2
1 , if x
2
≤ x ≤ x
3
1 +
x−x
3
x
4
−x
3
, if x
3
< x ≤ x
4
0 , else.
Remark. According to the definition of LR-type fuzzy
numbers made by (Dubois and Prade, 1979; Dubois
and Prade, 1988, 340) and explained by (Zimmer-
mann, 2005, 64), any fuzzy number
˜
M with


˜
M


≤ 4
can be expressed as a TrFN, as shown on table 1.
Table 1: Fuzzy numbers equivalence.
Fuzzy Number TrFN Equivalence
Fuzzy Singleton ( ¯x, ¯x, ¯x, ¯x)
Interval of Confidence (x
1
, x
1
, x
2
, x
2
)
TFN (x
1
, x
2
, x
2
, x
3
)
TrFN (x
1
, x
2
, x
3
, x
4
)
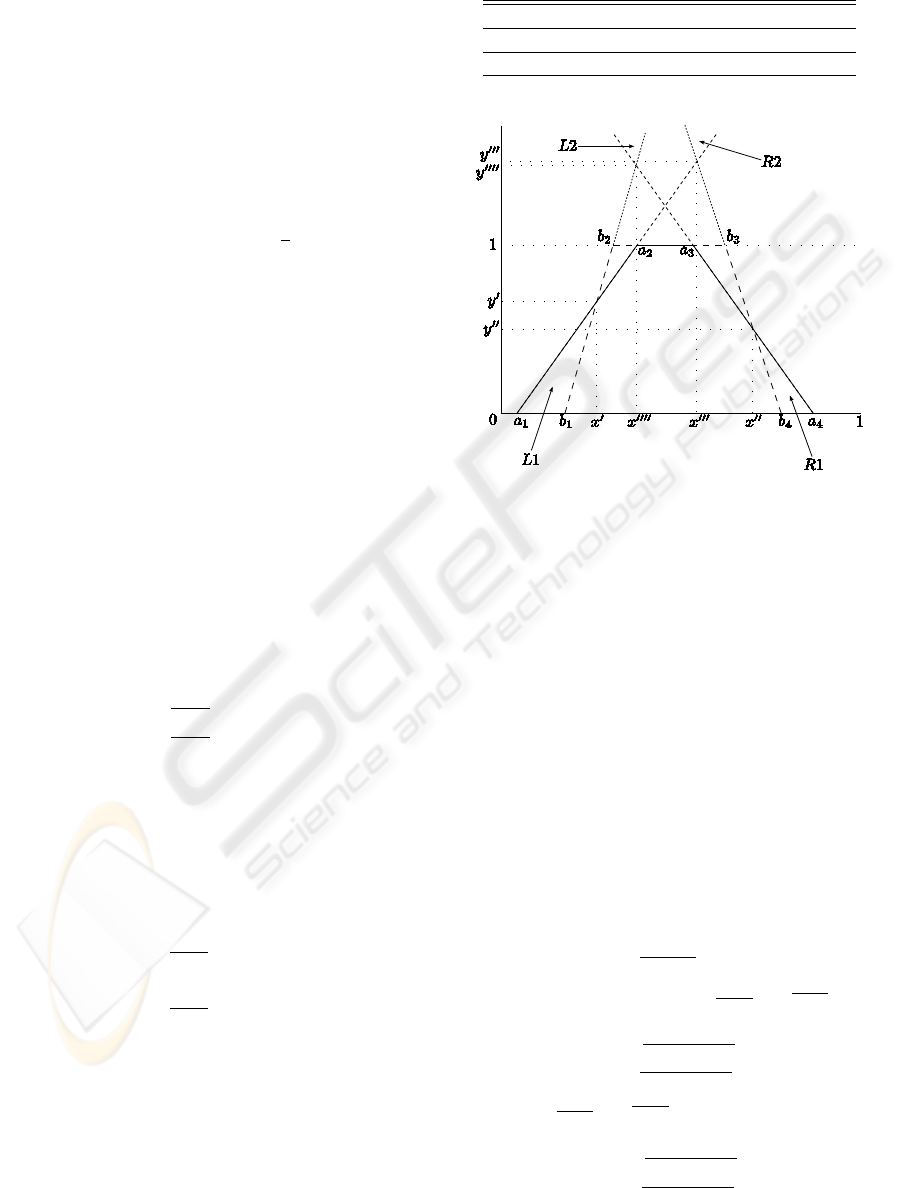
Figure 3: Distance between TrFN.
3 A WEIGHTED MEAN
HEMIMETRIC FOR Φ − FUZZY
SUBSETS
Let
˜
A = (a
1
, a
2
, a
3
, a
4
) and
˜
B = (b
1
, b
2
, b
3
, b
4
) be two
fuzzy numbers in the sense of definition 2.6, and
D

˜
A,
˜
B

a distance function between them. For the
purpose of this paper, this distance function implies
a sort of “projection” of
˜
A in
˜
B in the four regions
defined by L
1
, L
2
, R
1
and R
2
in figure 3.
Definition 3.1. For two TrFN
˜
A = (a
1
, a
2
, a
3
, a
4
) and
˜
B = (b
1
, b
2
, b
3
, b
4
), there are four intersection points,
{(x
0
, y
0
), (x
00
, y
00
), (x
000
, y
000
), (x
0000
, y
0000
)} which can be
found using the line equation:
y − y
1
=
y
2
− y
1
x
2
− x
1
(x − x
1
). (3)
For the intersection between a
1
a
2
and b
1
b
2
:
x
0
=
a
1
b
2
−b
1
a
2
b
2
−a
2
−b
1
+a
1
y
0
=
a
1
−b
1
b
2
−a
2
−b
1
+a
1
,
(4)
between a
3
a
4
and b
3
b
4
:
x
00
=
a
3
b
4
−b
3
a
4
b
4
−a
4
−b
3
+a
3
y
00
=
b
4
−a
4
b
4
−a
4
−b
3
+a
3
,
(5)
ICEIS 2009 - International Conference on Enterprise Information Systems
160

between a
1
a
2
and b
3
b
4
:
x
000
=
a
2
b
4
−a
1
b
3
b
4
−b
3
+a
2
−a
1
y
000
=
b
4
−a
1
b
4
−b
3
+a
2
−a
1
,
(6)
and between a
3
a
4
and b
1
b
2
:
x
0000
=
a
4
b
2
−a
3
b
1
b
2
−b
1
+a
4
−a
3
y
0000
=
a
4
−b
1
b
2
−b
1
+a
4
−a
3
.
(7)
Definition 3.2. The mean quadratic distance (MQD)
function for each region ζ of the set Z =
{L
1
, L
2
, R
1
, R
2
}, is calculated by:
D
ζ
=
R
β
ζ
α
ζ
(b
ζ
− a
ζ
)
2
dy
β
ζ
− α
ζ
, (8)
where a
ζ
is the equation of the line delimiting ζ on
the left, expressed in terms of y, b
ζ
is the equation of
the line delimiting ζ on the right, expressed in terms
of y, and {α
ζ
, β
ζ
} ∈ [0, 1], α
ζ
≤ β
ζ
, are the integration
limits in y for ζ, by definition 3.1 and figure 3, except
when a k b, where α = 0 and β = 1. For the purposes
of this paper, we want to measure the average distance
˜
A needs to be contained in
˜
B. For this reason, the
area of
˜
A that is already contained in
˜
B will generate
a MQD zero. As an example, the MQD from y
0
a
2
to
y
0
b
2
in figure 3 is equal to zero.
The solution for L
1
, R
1
, R
2
and L
2
are equations
(11), (12), (13) and (14), respectively.
Definition 3.3. The distance function D

˜
A,
˜
B

be-
tween two TrFN
˜
A = (a
1
, a
2
, a
3
, a
4
) and
˜
B =
(b
1
, b
2
, b
3
, b
4
) is:
D

˜
A,
˜
B

=
q
SD
N
, (9)
where:
SD=D
L
1
+D
L
2
+D
R
1
+D
R
2
N=1
(
D
L
1
>0
)
+1
(
D
L
2
>0
)
+1
(
D
R
1
>0
)
+1
(
D
R
2
>0
)
.
This distance function is a hemimetric because it
satisfies the following conditions:
1. D

˜
A,
˜
B

≥ 0
2. D

˜
A,
˜
C

≤ D

˜
A,
˜
B

+ D

˜
B,
˜
C

3. D

˜
A,
˜
A

= 0.
This hemimetric fails to satisfy the indentity of in-
discernibles, i.e., for any two TrFN
˜
A,
˜
B with
˜
A (
˜
B,
D

˜
A,
˜
B

= 0, even though
˜
A 6=
˜
B. Also, this hemi-
metric fails to satisfy the symmetry condition, i.e., for
any two TrFN
˜
A,
˜
B with
˜
A (
˜
B, D

˜
A,
˜
B

6= D

˜
B,
˜
A

,
because
˜
A ⊂
˜
B, but
˜
B 6⊂
˜
A.
Table 2: Candidate players assessments and “ideal” player
levels.
P
∼
1
P
∼
2
I
∼
[0.5,0.6,0.6,0.8] [0.4,0.4,0.5,0.5] [0.7,0.7,1.0,1.0]
[0.4,0.4,0.7,0.7] [0.8,0.8,0.8,0.8] [0.8,0.9,1.0,1.0]
[0.7,0.8,0.9,1.0] [0.5,0.7,0.9,1.0] [0.6,0.7,0.8,0.9]
Definition 3.4. Let P
∼
= {
˜
P
1
,
˜
P
2
, . . . ,
˜
P
n
} and I
∼
=
{
˜
I
1
,
˜
I
2
, . . . ,
˜
I
n
} be two Φ − fuzzy sets (Kaufmann and
Gupta, 1985, 125), i.e., both are sets of fuzzy num-
bers, and ω = {ω
1
, ω
2
, . . . ,ω
n
} a vector of weights
such that
∑
n
i=1
ω
i
= 1 and ω
i
6= 0. The weighted mean
hemimetric (WMH) between P
∼
and I
∼
will be:
δ

P
∼
, I
∼

=
n
∑
i=1
ω
i
D

˜
P
i
,
˜
I
i

(10)
4 EXAMPLE
A football
5
team manager needs to find a new mid-
fielder for his team. He would like to evaluate them
in three different variables:
1. Vision: ability to, in advance, visualize the devel-
opment of a play. The weight given to this vari-
able is ω
1
= 0.5.
2. Passing: ability to make a pass to the intended
place and player. The weight given to this vari-
able is ω
2
= 0.3.
3. Transfer Fee: the ammount of money needed to
bring this candidate to the team. The weight given
to this variable is ω
1
= 0.2.
He has two candidate players, P
1
and P
2
, to choose
from. From scouting reports and from his own expe-
rience, he has built, for each player, a Φ − fuzzy set
of the assessments in each of the three variables. He
has also constructed a model for the “ideal player” I
to compare with the candidates (see table 2).
We will calculate the WMH from P
1
to I as an
example:
D(
˜
P
1
1
,
˜
I
1
) =
r
0.02333 + 0 + 0 + 0.00333
1 + 0 + 0 + 1
= 0.11547
D(
˜
P
1
2
,
˜
I
2
) =
r
0.20333 + 0 + 0 + 0.02333
1 + 0 + 0 + 1
= 0.33665
5
Soccer.
THE SIGNING OF A PROFESSIONAL ATHLETE - Reducing Uncertainty with a Weighted Mean Hemimetric for Y -
Fuzzy Subsets
161

D
L
1
=











b
2
2
+b
1
b
2
−2a
2
b
2
−a
1
b
2
+b
1
2
−a
2
b
1
−2a
1
b
1
+a
2
2
+a
1
a
2
+a
1
2
3
, if a
1
≤ b
1
∧ a
2
≤ b
2
(b
1
−a
1
)
2
3
, if a
1
< b
1
∧ a
2
> b
2
(b
2
−a
2
)
2
3
, if a
1
> b
1
∧ a
2
< b
2
0 , if a
1
> b
1
∧ a
2
> b
2
.
(11)
D
R
1
=











b
4
2
+b
3
b
4
−2a
4
b
4
−a
3
b
4
+b
3
2
−a
4
b
3
−2a
3
b
3
+a
4
2
+a
3
a
4
+a
3
2
3
, if b
3
≤ a
3
∧ b
4
≤ a
4
(b
4
−a
4
)
2
3
, if b
3
> a
3
∧ b
4
< a
4
(b
3
−a
3
)
2
3
, if b
3
< a
3
∧ b
4
> a
4
0 , if b
3
> a
3
∧ b
4
> a
4
.
(12)
D
R
2
=





b
4
2
+b
3
b
4
−a
2
b
4
−2a
1
b
4
+b
3
2
−2a
2
b
3
−a
1
b
3
+a
2
2
+a
1
a
2
+a
1
2
3
, if a
1
≥ b
4
(b
3
−a
2
)
2
3
, if a
1
< b
4
∧ a
2
> b
3
0 , if a
2
≤ b
3
.
(13)
D
L
2
=





b
2
2
+b
1
b
2
−a
4
b
2
−2a
3
b
2
+b
1
2
−2a
4
b
1
−a
3
b
1
+a
4
2
+a
3
a
4
+a
3
2
3
, if a
4
≤ b
1
(b
2
−a
3
)
2
3
, if a
3
< b
2
∧ a
4
> b
1
0 , if a
3
≥ b
2
.
(14)
D(
˜
P
1
3
,
˜
I
3
) =
r
0 + 0 + 0.01 + 0
0 + 0 + 1 + 0
= 0.1
δ(P
∼
1
, I
∼
) = 0.5·0.11547+0.3·0.33665+0.2·0.1
= 0.1783
The WMH from P
2
to I is:
δ(P
∼
2
, I
∼
) = 0.16113.
As δ(P
∼
1
, I
∼
) > δ(P
∼
2
, I
∼
), the manager will prefer to
sign the second candidate over the first one to fill the
midfielder position.
5 CONCLUSIONS
We have presented a hemimetric for TrFN and a
weighted mean hemimetric for Φ − fuzzy sets, both
useful for human resources comparison in order to fill
an available position.
The hemimetric for TrFN was designed to take
into account the case where part or all of the first TrFN
area is contained in the second. In human resources
selection, once a particular feature of the candidate is
within the requirements to fill the position, there is no
need to calculate a distance. Therefore, the only thing
we need to know is how far the candidate is to the
level required in a particular feature.
By using Φ − fuzzy sets, we can extend this hemi-
metric to a large set of variables, in many different ar-
eas, each with a particular importance in the decision-
making process. The flexibility given to the team
manager allows him to overcome the natural uncer-
tainty in his work and gives an a strong base to his
decision.
The selection of human resources in professional
sport is an activity that should balance the economic
cost with the technical capability of the performers. A
failure in either area can lead to a fiasco. The recov-
ery of such problems is, by general rule, a task that
takes a long time, except for teams with the great-
est economic power. The shielding of a signing by
such techniques as the presented is absolutely neces-
sary given the present competitiveness of the sports
world.
REFERENCES
Borghesi, R. (2008). Allocation of scarce resources: Insight
from the NFL salary cap. Journal of Economics and
Business, 60:536–550.
Cannavacciuolo, A., Capaldo, G., Ventre, A., Volpe, A., and
Zollo, G. (1994). An approach to the evaluation of hu-
man resources by using fuzzy set theory. In Proceed-
ings of the Third IEEE Conference on Fuzzy Systems,
volume 2, pages 1165–1170.
Chen, S.-H. and Wang, C.-C. (2001). Representation, rank-
ICEIS 2009 - International Conference on Enterprise Information Systems
162

ing, distance, and similarity of fuzzy numberswith
step form membership function using k-preference in-
tegration method. IFSA World Congress and 20th
NAFIPS International Conference, 2001. Joint 9th,
2:801–806.
Chen, S.-H. and Wang, C.-C. (2007). House selection us-
ing fuzzy distance of trapezoidal fuzzy numbers. In
Proceedings of the Sixth International Conference on
Machine Learning and Cybernetics, Hong Kong.
Dubois, D. and Prade, H. (1979). Fuzzy real algebra: some
results. Fuzzy Sets and Systems, 2:327–348.
Dubois, D. and Prade, H. (1988). Possibility Theory: An
Approach to Computerized Processing of Uncertainty.
Plenum, New York.
Gil-Aluja, J. (1987). Selecci
´
on de Personal: el problema de
la polivalencia y el de la uniformidad. Number 6 in
Cuadernos de Econom
´
ıa Aplicada. Serie A. CEURA,
Madrid.
Gil-Aluja, J. (1996). La gesti
´
on interactiva de los recursos
humanos en la incertidumbre. CEURA, Madrid.
Gil-Lafuente, J. (1999). Optimization in signing of a player
in the sphere of uncertainty. In Proceedings of the In-
ternational Conference on Modelling and Simulation
MS’99, Santiago de Compostela.
Gil-Lafuente, J. (2000). A model for order in the purchase
preference for fixed assets in a sporting company. In
Proceedings of the International Conference on Mod-
elling and Simulation MS-2000.
Gil-Lafuente, J. (2001). El
´
ındice de m
´
aximo y m
´
ınimo
nivel en la optimizaci
´
on del fichaje de un deportista.
In Actas del X Congreso Internacional AEDEM.
Gil-Lafuente, J. (2005). Nuevo instrumento de selecci
´
on:
el ”
´
ındice de descartes por superaci
´
on-distancia”.
Cuadernos del SIMBAGE, 7:43–60.
Hanss, M. (2005). Applied Fuzzy Arithmetic: An Introduc-
tion with Engineering Applications. Springer, Berlin.
Hendricks, W., DeBrock, L., and Koenker, R. (2003). Un-
certainty, Hiring, and Subsequent Performance: The
NFL Draft. Journal of Labor Economics, 21(4):857–
886.
IOC Panel of Experts (2007). 1st Summer Youth Olympic
Games in 2010. Technical report, IOC.
James, B. and Henzler, J. (2002). Win Shares. STATS.
Kaufmann, A. and Gupta, M. M. (1985). Introduction to
Fuzzy Arithmetic. Van Nostrand Reinhold, New York.
Krautmann, A. and Oppenheimer, M. (2002). Contract
length and the return to performance in major league
baseball. Journal of Sports Economics, 3(1):6–17.
Massey, C. and Thaler, R. H. (2006). The Loser’s Curse:
Overconfidence vs. Market Efficiency in the National
Football League Draft. SSRN eLibrary.
Rojas-Mora, J. and Gil-Lafuente, J. (2008). The Tran and
Duckstein metric for fuzzy intevals of confidence in
the decision-making process of football teams. In
Proceedings of the International Conference on Mod-
elling and Simulation MS’08, Mallorca.
Sloane, P. J. (2006). Rottenberg and the Economics of Sport
after 50 Years: An Evaluation. SSRN eLibrary.
Yang, M.-S., Hung, W.-L., and Chang-Chien, S.-J. (2005).
On a Similarity Measure between LR-Type Fuzzy
Numbers and Its Application to Database Acquisi-
tion. International Journal of Intelligent Systems,
20(10):1001–1016.
Young, M. E. (2008). Nonlinear judgment analysis: Com-
paring policy use by those who draft and those who
coach. Psychology of Sport and Exercise, 9(6):760–
774.
Zadeh, L. A. (1965). Fuzzy sets. Information and Control,
8(3):338–353.
Zimmermann, H. (2005). Fuzzy Sets: Theory and its Appli-
cations. Springer, 4th edition.
THE SIGNING OF A PROFESSIONAL ATHLETE - Reducing Uncertainty with a Weighted Mean Hemimetric for Y -
Fuzzy Subsets
163