A QUADRATIC PROGRAMMING APPROACH TO THE
MINIMUM ENERGY PROBLEM OF A MOBILE ROBOT
Alain Segundo Potts*, José Jaime da Cruz* and Reinaldo Bernardi**
*Department of Telecommunications and Control, São Paulo University, São Paulo, Brazil
**Genius Institute of Technology, São Paulo, Dept. of Telecommunications and Control, São Paulo University, Brazil
Keywords: Mobile robots, quadratic programming, minimum energy, optimal control.
Abstract: As a consequence of physical constraints and of dynamical nonlinearities, optimal control problems
involving mobile robots are generally difficult ones. Many algorithms have been developed to solve such
problems, the more common being related to trajectory planning, minimum-time control or any specific
performance index. Nevertheless optimal control problems associated to mobile robots have not been
reported. Minimum energy problems subject to both equality and inequality constraints are generally
intricate ones to be solved using classical methods. In this paper we present an algorithm to solve it using a
Quadratic Programming approach. In order to illustrate the application of the algorithm, one practical
problem was solved.
1 INTRODUCTION
1.1 Preliminaries
Mobile robotics is an important research area and for
its study many researchers have dedicated a lot of
time to it. There are many problems in mobile robots
that are not present in industrial robots. Problems
with posture maintenance, localization, equilibrium
and energy consumption are common both at design
and operation times. Limbed robots can be
considered an important engineering conquest due to
the fact that they have larger mobility, flexibility and
freedom of movements than any other automatic
machine (Dudek, 2000). Research in this area
requires strong knowledge of mechanics, electronics,
computation, and eventually biomechanics. Limbed
robots are capable of walking and climbing and have
been developed around the world. (Armada et al.,
2003; Virk, 2005). Some of them have been used to
inspect bridges (Abderrahim et al., 1999) and
pipelines (Galves; Santos; Pfeiffer, 2001).
Presently the literature reports just two robots with
the ability of tree climbing. The first one was
developed at the Waseda University, Japan, and the
second one is the RiSE robots (Robots in Scansorial
Enviroments) (Saundersa et al., 2006) developed at
the United States. The RiSE robot is a member of a
new class of climbing robots whose design is based
on animals. For all of them, the energy consumption
is a big problem. Generally the battery is their
heaviest part since a considerable amount of energy
is necessary to drive the legs’motors.
Typically a leg has the form of a serial mechanism
with a highly nonlinear dynamics. This is one of the
reasons that make to find an optimal control law a
difficult problem. A second reason is the presence of
both equality and inequality constraints imposed on
the system – e.g., the actuator of each joint is subject
to saturation (Spont et al., 1989).
Many authors have worked in the optimization of
robots operation in the context of trajectory
planning. (Lin et al., 1983; Garg et al., 2002; Luo et
al., 2004). The problems considered in general
aimed to minimize the time or some quadratic
performance index. Nevertheless in the majority of
them both the Coriolis and Centrifugal terms were
omitted.
Optimal trajectory control systems usually can be
built by solving two associated sub-problems: i) the
optimal trajectory planning (OTP); ii) the trajectory
tracking control (TTC). Since there are many
complex constraints conditions concerning robot
kinematics and dynamics, the corresponding
245
Segundo Potts A., Jaime da Cruz J. and Bernardi R. (2008).
A QUADRATIC PROGRAMMING APPROACH TO THE MINIMUM ENERGY PROBLEM OF A MOBILE ROBOT.
In Proceedings of the Fifth International Conference on Informatics in Control, Automation and Robotics - RA, pages 245-251
DOI: 10.5220/0001499102450251
Copyright
c
 SciTePress

algorithms for solving the OTP problem have been
improved in recent years (Luo et al., 2004). Even
though good results have been obtained with the
OTP problem for both manipulators and industrial
robots, this is not the case for mobile robots.
A minimum energy formulation may be an
interesting approach for mobile robots, particularly
in applications where the battery weight is a critical
issue. Minimum energy problems may be difficult to
solve by classical methods since they involve both
the nonlinear dynamics of the robot and a set of
constraints.
In this paper a Quadratic Programming approach to
the minimum energy problem of a mobile robot is
proposed. The method is based on the discretization
of the problem. Numerical tests were performed for
Kamanbaré
1
, a robot currently under development at
the Automation and Control Laboratory (LAC),
University of São Paulo.
1.2 The Robotic Platform
Kamambaré is a biomimetic robotic platform, i.e., a
robotic platform inspired in nature, with the purpose
of climbing trees for environmental research
applications (see Fig. 1). More specifically the
platform locomotion is inspired in the form lizards
climb trees. The main characteristics sought in the
definition of the Kamanbaré platform were:
locomotion in irregular environments
(unpredictability of the branch complexity that
compose a tree), surmounting obstacles (nodes and
small twigs), tree climbing and descending without
risking stability, and keeping low structural weight
(mechanics + electronics + batteries). (Bernardi et
al., 2006)
Figure 1: Robot Kamanbaré.
1
Kamanbaré is the word in the Tupi indian language for
chameleon.
The prototype of the Kamanbaré platform presented
in this work was developed considering certain
capabilities (abilities), such as: locomotion in
irregular environments (unpredictability of the
branch complexity that compose a tree),
surmounting obstacles (nodes and small twigs), tree
climbing and descent without risking stability, and
keeping low structural weight (mechanics +
electronics + batteries). (Bernardi et al., 2006)
Each leg has three rigid links connected by two
rotational joints with one degree-of-freedom (d.o.f.)
each. The first link is connected to the platform by a
two d.o.f. rotational joint (Fig. 2).
Figure 2: Limb of the Kamanbaré Platform.
All joins are controlled by DC motors. The control
problem for mobile robot is the problem of
determining the time history of join required to
cause the end-effectors (the gripper) executed a
commanded motion.
There are many control techniques and
methodologies that can be applied to the control of
limbed robots. The particular control method chosen
as well as the manner in which it is implemented can
have a significant impact on the performance of the
robot and consequently on the range of its possible
applications. Optimal control of energy can be an
interesting policy when the robot must operate
autonomously for a long time. The control problem
for the tree climbing robot considered here is to
determine the time history of each limb joint
required to cause the leg to move from an initial
angle to a final one in such a way that the energy
loss in the motors is minimal.
ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics
246

2 FORMULATION AND
SOLUTION OF THE OPTIMAL
CONTROL PROBLEM
2.1 The State Space Model
This work consider the control strategy named
independent joint control. In this type of control
each axis of the limb is controlled as a single input
/single output system. Any coupling effects due to
the motion of the others links is either ignored or
treated as a disturbance. (Spont et al., 1989)
The space state model that describes the dynamics of
the DC motor located at the i-th joint (
ni
≤
≤1 ) of
the leg can be expressed by the equations:
BuAxx
+
=

(1)
τ
EDuCxy ++=
(2)
where
⎥
⎦
⎤
⎢
⎣
⎡
−
=
Jb
A
/0
10
,
(3)
⎥
⎦
⎤
⎢
⎣
⎡
=
JK
B
m
/
0
,
(4)
[]
ab
RKC /0 −= ,
(5)
a
RD /1= ,
(6)
()
ma
KRrE /= ,
(7)
and
m
m
x
θ
θ
⎡⎤
=
⎢⎥
⎣⎦

,
(8)
m
r
uV
K
τ
=−
.
(9)
J
is the moment of inertia of the rotor,
b
is the
viscous damping coefficient of the mechanical
system,
V is the armature voltage (control variable),
a
R
is the armature resistance,
a
iY = is the
armature current,
m
K
is the torque coefficient of the
motor,
b
K
is the counter-electromotive coefficient,
τ
is the load torque, 1
<
r
is the gear reduction
factor,
m
θ
is the angular position of the rotor and
m
θ

is the angular speed of the rotor. Notice that the
input variable
u depends on both the control
variable
V
and the load torque
τ
, which also
depends on
V through
m
θ
and
m
θ

.
The load torque
τ
, which depends on the robot
dynamics, is given by : (Spong, 1989)
(
)
(
)
[
]
(
)
(
)
2
iz
M
qq Bq qq Cq q Gq τ
⎡⎤
=+ + +
⎣⎦
   
(10)
where
(
)
M
q
is the leg inertia matrix,
(
)
Bq
is the
Coriolis torque matrix,
(
)
Cq
is the centrifugal
torque matrix,
(
)
Gq
is the gravitational torque
vector,
[
]
[
]
12 13 1
T
iz n n
qq qq qq q q
−
=
    
…
,
:1 ,1iz in zn
∀
≠<<<<
222 2
12
⎡
⎤⎡ ⎤
=
⎣
⎦⎣ ⎦
 
…
T
n
qqq q
and
[
]
T
n
qqqq …
21
=
,
where
i
q , ni
≤
≤
1 , is the generalized coordinate
of joint
i and n is the number of joints of the leg.
Some dynamical effects like friction were not
included in (10) although they may be significant for
some limbs. In addition, a more detailed model of
the leg dynamics could include various sources of
flexibility, defection of the links under load and
vibrations (Borrow et al., 2004). Nevertheless, this
model is sufficiently accurate for our purposes since
these effects are not significant for the leg under
consideration.
One of the characteristics of the independent joint
model is that
τ
is multiplied by the gear
reduction
r . Thus effect of the gear ratio is to
reducing the coupling nonlinearities presents in
dynamics of the limbs.
The solution to equation (1) is given by:
() ( )
()
()
0
0
t
At
At
x
tex e Bu d
ς
ς
ς
−
=+
∫
(11)
2.2 The Optimal Control Problem
In this section it is assumed that τ (t) is known for all
t in the interval [0 t
f
]. The performance index
adopted is the Joule loss in the armature resistance
of each motor during the motion:
A QUADRATIC PROGRAMMING APPROACH TO THE MINIMUM ENERGY PROBLEM OF A MOBILE ROBOT
247

∫
=
f
t
dtP
0
min ε
(12)
where
f
t
is the time required to move the joint from
the initial to the final position, and
P is the power
dissipated:
where
Y was defined in (2).
The optimal control problem is subject to the
following constraints:
() () ()
2
1
b
m
aaam
K
r
x
tut tI
RRRK
τ −++ ≤
,
(14)
() () ()
2
1
b
m
aaam
K
r
I
xt ut t
RRRK
τ
−≤− + +
,
(15)
(
)
mm
VutV−≤ ≤
,
(16)
()
1
f
f
x
tqr=
,
(17)
(
)
2
0
f
xt =
,
(18)
where
m
I and
m
V are, respectively, the maximum
armature current and maximum armature voltage of
the motor and
0
f
tt
⎡⎤
∈
⎣⎦
. With no loss of
generality we take
1
(0) 0x =
. Considering the motor
initially at rest,
2
(0) 0x =
.
This type of problem is hard to solve and generally
involve a great computational effort (Kirk, 1998).
Mobile robots require a quick solution and to solve it
in real-time is practically impossible. These are
among the reasons for which we decided to look for
another kind of solution.
2.3 Discretization
Let us to define the time-step as:
1
f
kk
t
ttt
N
−
Δ= = −
(1 )kN<≤
(19)
where
N can be chosen sufficiently large to
discretize
f
t . Then it is assumed that
(
)
ut
is a
stepwise constant function and
k
u is used to denote
the value of
(
)
ut
for all t in the k -th time interval
1
[,)
kk
tt
−
.
Taking into account equations (11), (12), (13) and
(19), the functional
ε
can be rewritten as:
2
11
min
NN
kaa
kk
P
tRit ε
==
=
Δ= Δ
∑∑
(20)
and the solution of system (1) as:
(
)
k
At
kk
x
teIU=Γ
(21)
where,
12
1
00
N
N
t
tt
AA A
t
eBd eBd eBd
ςς ς
ς
ςς
−
−− −
Γ= + + +
∫∫ ∫
…
,
(22)
[
]
12
T
N
Uuu u= …
(23)
and
1
2
000
000
00 0
000
k
n
e
e
I
e
⎡
⎤
⎢
⎥
⎢
⎥
=
⎢
⎥
⎢
⎥
⎣
⎦

(24)
Where
i
e = 1 for 1 ik
≤
≤ and
i
e = 0 for
kiN
<
≤ .
Matrix
Γ
can be calculated offline since it depends
only on the motor parameters.
From equations (20) and (21) it is possible rewrite
(20) as:
where matrices
Q and K depend only on the motor
parameters and
σ
is a constant. The constraints for
the problem are:
2
1
k
b
mkkm
aaam
K
r
Ixu I
RRRK
τ
−
≤− + + ≤
(26)
mkm
VuV
−
≤≤
(27)
1
N
f
x
qr
=
(28)
2
0
N
x
=
(29)
where constraints (26) and (27) apply for all
k ,
.1 Nk
≤
≤
Since
σ
is a constant, it is not relevant for the
optimization.
[
]
[
]
22
'' '' ''
aa a a
P
Ri RY R xC u D E Cx Du E
τ
τ == = ++ ++
(13)
()
1
min
2
TT
UUQUKU
ε
τσ
=
++
(25)
ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics
248

The problem given by equations (25)-(29) has thus
the form of a Quadratic Programming problem
which is certainly the kind of nonlinear
programming problem closest to linear programming
from analytical and computational point of view.
Solution for this kind of problem can be efficiently
found by numerical methods. (Avriel, 1976)
(Winston, 1995).
2.4 The Algorithm
An iterative algorithm to solve the minimum energy
problem based in equations (13) and (20) is
proposed in this section.
To start the algorithm it is assumed that
0:
0
≡=
kk
τ
τ
for all k , .1 Nk ≤≤ Then
Quadratic Programming problem of minimizing the
function (20) subject to constraints (26) to (29) is
solved. Denote by
0*
k
U the optimal solution for this
problem. Using equation (17) and recalling equation
(1), both the motor angular position
)(
0
k
m
θ
and
angular speed
)(
0
k
m
θ

can be evaluated for all k ,
.1 Nk ≤≤
The second step of the algorithm begins by using the
leg dynamical equations (10) to evaluate a new
torque time history
1
k
τ
for all
k
,
.1 Nk ≤≤
The
new Quadratic Programming problem is then solved
and
1*
k
U is obtained. )(
1
k
m
θ
and )(
1
k
m
θ

are
evaluated for all
k , .1 Nk
≤
≤
The process is repeated until
1jj
kk
τ
τ
τε
+
−< for a
given accuracy
τ
ε
and two consecutive steps j and
j+1. When convergence is attained the optimal
vector of armature voltages
*1+j
V
can be evaluated
using equation (9).
The algorithm is expected to converge since the gear
reduction ratio
r is generally small and the effect of
the torque on the motor dynamics is correspondingly
small too.
The algorithm may thus be summarized as:
Algorithm
0
0
1
k
j
τ
=
=
−
repeat
1
j
j
=
+
()
*
1
min
2
: (26) to (29)
001
0
TjT
k
jjj
kkk
m
UUQUKU
subject to constrains equations
xxU
K
b
J
J
ετ
⎧
=+
⎪
⎨
⎪
⎩
⎡⎤
⎡⎤
⎢⎥⎢⎥
=+
⎢⎥
⎢⎥
−
⎣⎦
⎣⎦

[][]
() ()
[]
() ()
12
TT
jj
kk
j
k
qqq rxxx
M
qq Bq qq Cq q Gq τ
+
=
⎡⎤
=+ + +
⎣⎦
 
   
until
(
)
(
)
1
max
jj
kk
τ
τ
τε
+
−≤
3 SIMULATION RESULTS
This section presents the results obtained from the
application of the algorithm above to a leg similar to
that of the Kamanbaré platform.
The algorithm code was written in MatLab. The
following data were used:
2=
f
ts
,
10
=
N
,
11
10
−
=
τ
ε
and
012
0
4
NN N
T
T
mmm
π
θθθ π
⎡⎤
⎡⎤
=−
⎢⎥
⎣⎦
⎣⎦
Algorithm convergence occurred in 15 iterations.
Table 1 shows the algorithm steps until the optimal
solution is reached. The overall processing time was
quite small.
Figure 3 show the optimal solution
*
15
k
U
for each
motor.
0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 2
-0.5
0
0.5
Optimal Control
Voltage 1 [volts]
0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 2
-0.1
0
0.1
Optimal Control
Voltage 2 [volts]
0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 2
-0.1
0
0.1
Optimal Control
Voltage 3 [volts]
Time [s]
Figure 3: Optimal Solution.
A QUADRATIC PROGRAMMING APPROACH TO THE MINIMUM ENERGY PROBLEM OF A MOBILE ROBOT
249

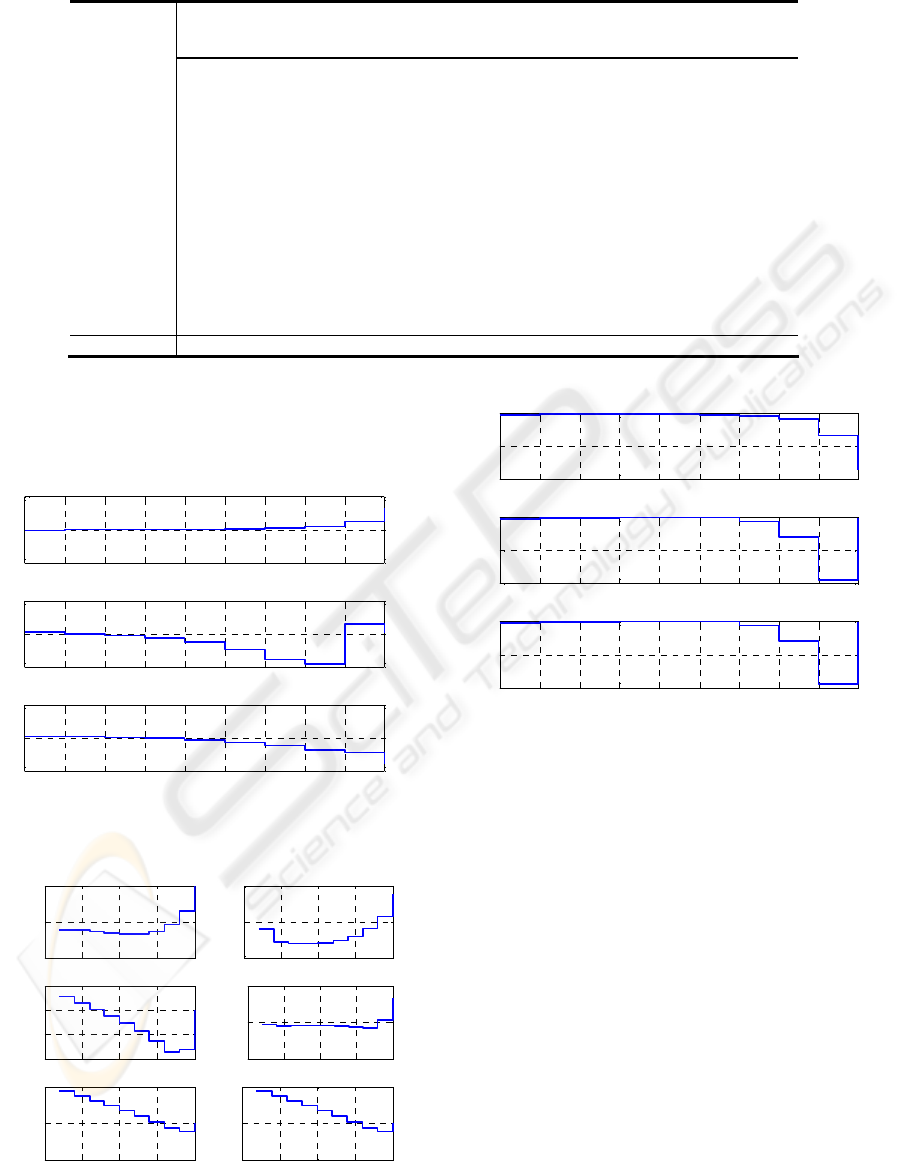
Table 1: Minimum Energy Consumption.
Energy Consumption
1
N
k
k
Pt ε
=
=
Δ
∑
[watts]
Iteration (j)
Joint 1 (Motor 1) Joint 2 (Motor 2) Joint 3 (Motor 3)
1 0.22583525809518 0 0.01411470363095
2 0.54691612008194 0.00249201214070 0.02563789026998
3 0.60424685648279 0.00151916407557 0.02084265484899
4 0.60913169232854 0.00162074115964 0.02201351589222
5 0.60878562782495 0.00159940182719 0.02201765824694
6 0.60878328339302 0.00160200730314 0.02202687314770
7 0.60877614492969 0.00160176202487 0.02202629388348
8 0.60877639908587 0.00160179288124 0.02202637161877
9 0.60877635993567 0.00160178879636 0.02202635576755
10 0.60877636906069 0.00160178928402 0.02202635725193
11 0.60877636847905 0.00160178921712 0.02202635705179
12 0.60877636859543 0.00160178922523 0.02202635707836
13 0.60877636858174 0.00160178922422 0.02202635707548
14 0.60877636858322 0.00160178922435 0.02202635707588
15 0.60877636858300 0.00160178922433 0.02202635707583
Figures 4 and 5 show kinematics of each joint; the
angular position and the speed and acceleration
achieved for the optimal control
*
15
k
U
.
0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 2
-5
0
5
rad
Join Position 1
0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 2
-0.1
0
0.1
rad
Join Position 2
0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 2
-1
0
1
rad
Join Position 3
Time [ s]
Figure 4: Joints Positions.
0 0.5 1 1.5 2
-0.1
-0.05
0
Angular Speed
[rad/s]
0 0.5 1 1.5 2
0
0.1
0.2
Angular Acceleration
[rad/s
2
]
0 0.5 1 1.5 2
-0.02
-0.01
0
0.01
[rad/s]
0 0.5 1 1.5 2
-0.1
0
0.1
[rad/s
2
]
0 0.5 1 1.5 2
-0.05
0
0.05
[rad/s]
Time [s]
0 0.5 1 1.5 2
-0.05
0
0.05
[rad/s
2
]
Time [ s ]
Figure 5: Speed’s Joints and Acceleration’s Joints.
0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 2
-10
0
10
τ
[n]
Torque 1
0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 2
-4
-2
0
τ
[n]
Torque 2
0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 2
-4
-2
0
Tim e[s]
τ
[n]
Torque 3
Figure 6: Torques for each motor.
In this particularly case the motor’s 2 and 3 have the
same torque.
4 CONCLUSIONS
This paper discussed the formulation and solution of
an important problem related to mobile robotics: the
minimum energy loss problem.
An optimal control problem was formulated to
represent this case. After discretization in time the
optimal control problem was rewritten in the form of
a Quadratic Programming problem whose solution
could be obtained efficiently. The algorithm was
tested for a leg similar to that of the Kamanbaré
platform.
Although the whole problem is nonlinear and quite
complex the algorithm converged quickly in all the
ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics
250

tests performed by now. It is thus expected that the it
can be used to operate in real-time.
REFERENCES
Abderrahim, M., Balaguer, C., Gimenez, A., Pastor, J. M.,
Padrón, V. M., 1999. ROMA: A Climbing Robot for
Inspection Operations. In, Proceedings of the IEEE
International Conference on Robotics and
Automattion, Vol 3, pp 10-15.
Armada, M., Santos, P. G. de, Jiménez, M. A., Prieto, M.
2003. Application of CLAWAR Machines. In, The
International Journal of Robotics Research. Vol. 22,
nº3–4, pp. 251-264.
Avriel, M, 1976. Nonlinear Programming. Analysis and
Methods. Prentice-Hall. New Jersey, 1
st
edition.
Bernardi, R., Cruz, J.J. 2006. KAMANBARÉ. A tree-
climbing biomimetic robotic platform for
environmental research. In, International Conference
on Informatics in Control, Automation and Robotics.
Bobrow, J.E., Park, F.C., Sideris, A. 2004. Recent
Advances on the Algorithmic Optimization of Robot
Motion. Departament of Mechanical and Aerospace
Engineering, University of California.
Dudek, G., Jenkin, M., 2000. Computational Principles of
mobile Robotics. Cambridge Press. 1
st
edition.
Galvez, J. A., Santos, P. G. de, Pfeiffer, F., 2001. Intrinsic
Tactile Sensing for the Optimization of Force
Distribution in a Pipe Crawling Robot. In,
IEEE/ASME Transactions on Mechatronics, Vol. 6,
n°1.
Garg, D. P., Kumar, M., 2002. Optimization Thecniques
applied to multiple manipulators for path planning
and torque minimization. In Eng. Applications Art,
Int., Vol 15, pp 241-252.
Kirk, D., 1998. Optimal Control Theory an Introduction.
Dover Publication, New York, 2
nd
edition.
Lin, Ch., Chang P., Luh, J.Y.S. 1983 Formulation and
Optimization of Cubic Polynomial Joint Trajectories
for Industrial Robots. In IEEE Transactions on
Automatic Control, Vol AC-28, No 12, December.
Luk, B., Cooke, D., Galt, S., Collie, A., Chen, S. 2005.
Intelligent legged climbing service robot for remote
Maintenance applications in hazardous environments.
In Robotics and Autonomous Systems. Accepted June
2005.
Luo, X., Fan, X., Zhang, H., Chen T., 2004. Integrated
Optimization of Trajectories Planning for Robots
Manipulators Based on Intensified Evolutionary
Programming. Proceedings of the 2004 IEEE,
International Conference on Robotics and
Biomimetics.
Saundersa, A., Goldmanb, D., Fullb,R., Buehlera, M.
2006. The RiSE Climbing Robot: Body and Leg
Design. In, Proceeding of SPIE, Vol. 6230, 623017.
Spong, M., Vidyasagar, M., 1989. Robot Dynamics and
Control. John Wiley & Sons, Canada, 1
st
edition.
Virk, G. S. 2005. The CLAWAR Project: Developments in
The Oldest Robotics Thematic Network. IEEE
Robotics & Automation Magazine, pp. 14-20.
Winston, W. 1995. Introduction to Mathematical
Programming. Applications and Algorithms. Duxbury
Press. California, 2
nd
edition.
A QUADRATIC PROGRAMMING APPROACH TO THE MINIMUM ENERGY PROBLEM OF A MOBILE ROBOT
251