ROBUST ADAPTIVE WAVELET NEURAL NETWORK TO

CONTROL A CLASS OF NONLINEAR SYSTEMS

A. Hussain, N. Essounbouli, A. Hamzaoui

CReSTIC, IUT de Troyes,9 rue de Québec, Troyes, France

J. Zaytoon

CReSTIC, Uiversité de Reims Champagne-Ardenne, Reims, France

Keywords: Adaptive control, adaptive wavelet neural network systems, adaptive identification, nonlinear systems,

sliding mode control.

Abstract: This paper deals with the synthesis of a Wavelet Neural Network adaptive controller for a class of second

order systems. Due to its fast convergence, the wavelet neural network is used to approximate the unknown

system dynamics. The proposed approximator will be on-line adjusted according to the adaptation laws

deduced from the stability analysis. To ensure the robustness of the closed loop system, a modified sliding

mode control signal is used. In this work, variable sliding surface is considered to reduce the starting energy

without deteriorating the tracking performances. Furthermore, the knowledge of the upper bounds of both

the external disturbances and the approximation errors is not needed. The global stability of the closed loop

system is guaranteed in the sense of Lyapunov. Finally, a simulation example is presented to illustrate the

efficiency of the developed approach.

1 INTRODUCTION

In last decade, active research has been carried out

in neural network control (

Omidvar, 97) (Noriega, 98)

(

Lin, 98). The characteristics of fault tolerance,

parallelism and learning suggest that they may be

good candidates for implementing real-time adaptive

control for nonlinear dynamical systems. It has been

proven that an artificial neural network can

approximate a wide range of nonlinear functions to

any desired degree of accuracy under certain

conditions (

Omidvar, 97). It is generally understood

that the selection of the neural network training

algorithm plays an important role for most neural

network applications. In the conventional gradient-

descent-type weight adaptation, the sensitivity of the

controlled system is required in the online training

process (

Lin, 98). However, it is difficult to acquire

sensitivity information for unknown or highly

nonlinear dynamics. Moreover, the local minimum

of the performance index remains variable (

Omidvar,

97). In practical control applications, it is desirable

to have a systematic method for ensuring the

stability, robustness, and performance properties of

the overall system. Recently, several neural network

control approaches have been proposed based on

Lyapunov stability theory (

Fabri, 96) (Farrell, 98)

(Seshagiri, 00). One main advantage of these control

schemes is that the adaptive laws were derived based

on the Lyapunov synthesis method and therefore, the

stability of the control system is guaranteed.

However, some constraint conditions should be

assumed in the control process, e.g., the

approximation error, optimal parameter vectors, or

higher order terms in a Taylor series expansion of

the nonlinear control law are bounded. Also, the

prior knowledge of the controlled system may be

required, e.g., the external disturbance is bounded or

all states of the controlled system are measurable.

These requirements are not easy to satisfy in

practical control applications. Recently, Wavelet

Neural Networks (WNN) have became a very active

subject in many scientific and engineering research

areas (Zhang, 95) (Kostka, 00) (Lin, 03) (Ho, 05).

The WNN have been proposed as a universal tool

for functional approximation, which combine the

capability of artificial neural networks in learning

Hussain A., Essounbouli N., Hamzaoui A. and Zaytoon J. (2007).

ROBUST ADAPTIVE WAVELET NEURAL NETWORK TO CONTROL A CLASS OF NONLINEAR SYSTEMS.

In Proceedings of the Fourth International Conference on Informatics in Control, Automation and Robotics, pages 60-67

DOI: 10.5220/0001640400600067

 SciTePress

and the capability of wavelet decomposition. The

WNN allows resolving the conventional problem of

poor convergence or even divergence encountered in

other kinds of neural networks. It can also increase

convergence speed (Delyon, 95) (Hsu, 06).

Sliding mode control is unique in its ability to

achieve accurate, robust, decoupled tracking for a

class of nonlinear time-varying systems in the

presence of disturbances and parameter variations

(Utkin, 77) (Salamci, 01). The tracking of the

desired trajectory is achieved through two phases: an

approach phase, where the system is controlled to

attain a predefined sliding surface, and a sliding

phase along the sliding surface. However, in order to

deal with the presence of modelling imprecision and

disturbances, the control law has to be discontinuous

across the sliding surface. Since the implementation

of the associated control switching is necessarily

imperfect, this leads to chattering which involves

high control activity and may excite high-frequency

dynamics and can, therefore, damage the plant

(Slotine, 91). To resolve this problem, many

solutions have been proposed in the literature

(Slotine, 91)- (Lin, 02) (Berstecher, 01) (Hwang, 01)

(Lin, 95) (Wai, 04). In (Slotine, 91), a boundary-

layer in the neighbouring of the sliding surface has

been defined to obtain a continuous behaviour of the

control signal across this surface. Based on the same

idea, a fuzzy system has been used to define this

boundary layer and to exploit the human knowledge

(Lin, 02). To remove the discontinuity in the control

signal, some approaches combining sliding mode

control and classical controller using a fuzzy

supervisor can be cited (Berstecher, 01) (Hwang, 01)

(Lin, 95). These methods resolve the problem related

to the chattering phenomenon. However, to design

the switching signal assuring the approaching phase,

the upper bounds of both the external disturbances

and the structural uncertainties must be well known.

To overcome these problems, the authors of

(Hamzaoui, 04) (Wai, 04) have proposed an

approximation of the switching signal by an adaptive

fuzzy system to eliminate the chattering

phenomenon without requiring any particular

knowledge about the upper bounds of both

approximation errors and external disturbances.

Nevertheless, the global stability of the closed loop

system in these approaches is guaranteed only for a

good approximation level or for a particular choice

of the initial values of the adjustable parameters.

This paper proposes a wavelet Neural Network

Adaptive Control (WNNAC) for a class of second-

order nonlinear, uncertain and perturbed systems;

this controller combines the advantages of WNN

identification and the robustness of sliding mode

control. The control law is composed of two parts.

The first one represents the WNN identifier that

perform the online system dynamic function

estimation. This identifier is adjusted according

some adaptations laws deduced from the stability

analysis. The second part of the control law

represents the robust term which ensure the

robustness of the closed loop system in the sense of

sliding mode technique. This term is synthesised

such that knowing of the upper bounds of the

external disturbances is not required. Furthermore,

the proposed control law uses a variable sliding

surface to reduce the starting energy obtained by a

classical sliding surface. The stability of the closed

loop system is stated using the Lyapunov theory. To

illustrate the efficiency of the proposed approach, a

numerical simulation example is considered.

The paper is organised as follows: Section 2

illustrates the description of WNN networks. Section

3 is dedicated to the formulation and the

investigation of the control problem. In section 4, we

present the synthesis of the proposed controller

whose design procedure is explained in section 5. To

show the efficiency of the proposed approach, a

simulation example is presented in section 6.

2 DESCRIPTION OF WAVELET

NEURAL NETWORKS (WNNS)

Wavelet neural networks are special case of feed-

forward neural networks. The main difference

between the artificial neural networks (ANN) and

WNN is that, in ANN the nonlinearities are

approximated by superposition of sigmoid functions.

However, in WNN, nonlinearities are approximated

by superposition of wavelet functions (Oussar, 98).

Similar to ANN, WNN are also shown to have

universal approximation property (Yoo, 05)

(Sureshbabu, 99).

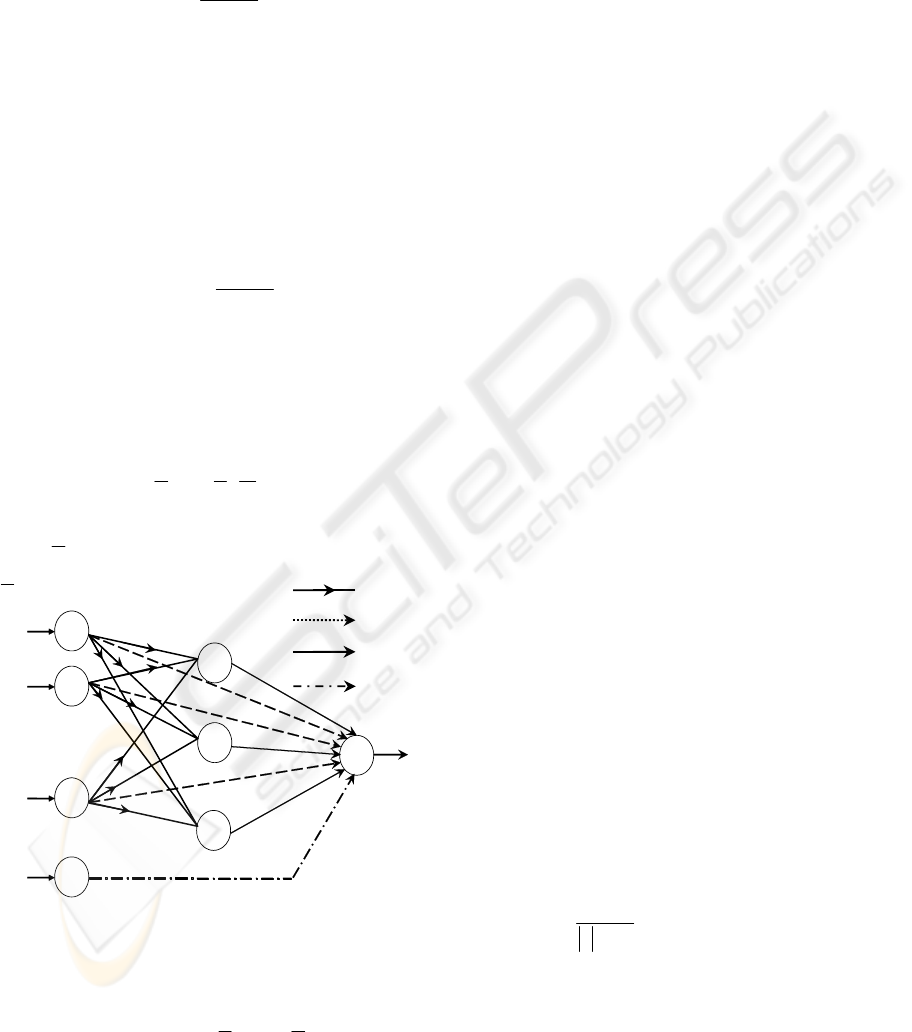
Similar to the ANN, the WNN consists of an

input layer, a hidden layer, and an output layer. The

WNN model structure shown in Figure 1 consists of

'n' input neurons

(,,,)

xx… in the input layer,

equal to the number of input variables. The input

neurons are connected to the next layer of neurons,

called the hidden layer neurons which make use of

wavelets as transformation functions. These neurons

are termed as "wavelons". In this work, the Mexican

hat (1) is used as a 'mother' wavelet

( ) (1 ) exp( 0.5 )

=− × −

(1)

ROBUST ADAPTIVE WAVELET NEURAL NETWORK TO CONTROL A CLASS OF NONLINEAR SYSTEMS

Several daughters of wavelets

can be constructed

by translating and dilating the mother wavelet

according to (2).

()

ψψ

⎛⎞

−

⎜⎟

⎝⎠

(2)

where

ij i

∑

is input scaling vector

while

, and

represent the translation and

dilation factors of the wavelet.

For i and j represent the indices of input, hidden, and

output layers respectively, the output from the

hidden wavelon,

is given by (3).

()

⎛⎞

−

⎜⎟

⎝⎠

∑

(3)

This output is connected directly to the output layer

neurons. The output layer usually consists of a linear

output neuron. Mathematically, the final production

obtained from figure 1 can be represented by (4).

output

YCAXB=Ψ+ +

(4)

with

[]

Cc c=  ,

[

]

HΨ=  and

[]

aa= 

Figure 1: The structure of the used WNN.

The approximator in figure 1 includes three

independent adaptable parts; constant, linear and

non-linear given by

B ,

and C respectively.

Thus, the approximator (4) is able to estimate

efficiently all possible systems static or dynamics by

managing learning rate of each part.

3 PROBLEM STATEMENT

Consider the following 2

order system:

(,) (,)yfyygyyud

  

(5)

where

and

are two unknown continuous

functions.

u and y designate the input and output

of the system respectively while

d is an external

disturbance assumed to be unknown but bounded.

The input-output system (5) includes a large class of

non-linear second-order systems likes Duffing

oscillator and mass-spring-damper system

(Bartoloni, 97) (Roup, 01) (Chang, 05).

In this work, we assume that the function

(, )



can be written as a sum of a known nominal

term and an uncertain as follows

(,) (,) (,)

yy g yy yy



In this case, equation (5) can be rewritten as:

(,) (,)

yfyygyyu

  

(6)

where

The objective of this work is to synthesize a

robust controller, based on sliding mode, able to

force the output of the system y to follow a bounded

reference trajectory

y under the constraint that all

involved signals are bounded.

We denote the tracking error by

ey y=− and the

sliding surface by:



(7)

Since using a large value of the slop

gives a fast

system response. However, a too large value can

lead to overshoot and even instability. From the

other side, small value of

results a slow system

response. To overcome this problem, the slope can

be adapted according to tracking error value

()et (Liu, 05). In this case, equation (7) becomes

()

eee



(8)

where

()

is a given positive constant

and

is a small positive scalar given by the

designer.

Differentially according time of equation (8) gives

() () () ()

() ()

st et et et

y y et et

λλ

=+ +

=−+ +



 



  

(9)

Bias

output

ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics

Using (6), equation (9) becomes

() () ()

tyfgu et et

δλ λ

=−− −+ +



 

(10)

() () ()

tf etguyet

δλ λ

=− − + − + +





(11)

() ( , , ) ()

t Fyyy gu y et

=− − + +

 

(12)

where

(,, ) ()

yyy f et

δλ

=+ −



In the next section, the problem of

(,, )

yyy



term

estimation will be treated

4 THE WNN ADAPTIVE

CONTROLLER SYNTHEISIS

It is worthy to say that if the system output and its

time derivative converge to their reference signal,

the unknown function

(,, )

yyy



goes

(,)



. To approximate (,, )

yyy



we can

use a WNN in the form

(,)

dd d

yy C AY B

=+ +



with

y and



as inputs (Chang, 05).

Consider the pre-assigned constraint regions of

C ,

and B defined respectively as:

{}

/,0

Ccc

CC MMΩ= ≤ >

{}

/,0

AAA

AA M MΩ= ≤ >

{}

/,0

BBB

BB M MΩ= ≤ >

According to the approximation theorem, there

exists a finite optimal value of

(,)



noted by:

***

(, )

dd d

yy C AY B

=+ +



(

C ∈Ω ,

A∈Ω and

∈

Ω ) such that:

(, ) (, )

Fdd dd

yy Fyy

=−



hence, equation (12) can be rewritten as:

() ( , )

()

dd F d

tFyy guy

λδ

=− + − +

 



(13)

To guarantee the global stability of the closed loop

system and the convergence of the tracking error to

zero, we propose the following control law:

() ( , )

dd d

ut g F y y y e

−

⎡⎤

=− +++

⎢⎥

⎣⎦

 

(14)

Substituting (14) in (13) yields to:

ˆˆ

() ( , ) ( , )

dd dd d

dFd

tFyyFyyy

ey e

λλδδ

=− + −

−++++−



 

(15)

which can be rewritten as

()

tC AyB

δδ

++−







(16)

To study the stability of the closed loop system and

to find the adaptation laws for the adjustable

parameters, we consider the following Lyapunov

function:

11 1 1

()

22 2 2

CA B

vt s C C A A B

γγ γ

=+ +

 



(17)

The time derivative of

()vt is given by:

11 1

()

CA B

vt ss C C A A BB

γγ γ

=+ +





 





(18)

Substituting (16) in (18) gives:

()

11 1

dFd

CA B

vt s C A y B

CC AA BB

ψδδ

γγ γ

⎛⎞

=++++−

⎜⎟

⎝⎠











 



()

Fd C

Ad B

vt s s C C s

Asy BBs

δγψ

γγ

=+−+ +

++++







(19)

Choosing the following adaptation law

=−



(20)

=−



(21)

=−



(22)

leads to:

()

vt s s

δδ

=+−



(23)

() 2

ρδ

=− + −

+−



(24)

ROBUST ADAPTIVE WAVELET NEURAL NETWORK TO CONTROL A CLASS OF NONLINEAR SYSTEMS

22 22

()

ρδ ρδ

ρρ

ρδ ρδ

⎛⎞⎛⎞

=− − − −

⎜⎟⎜⎟

⎝⎠⎝⎠

++−



(25)

222

()

δρδ

≤− + +



(26)

Let

μμ

⎧⎫

⎪⎪

Ω= ≤ >

⎨⎬

⎪⎪

⎩⎭

According to the regions

Ω ,

Ω and

there is a sufficient large constant

max

V such that

max

max , , , ( )

SC A B

sC A B

Vvt

∈Ω ∈Ω ∈Ω ∈Ω

≤

(Chang-05).

Afterward, we can define

max

⎧⎫

⎪⎪

Ω= ≤

⎨⎬

⎪⎪

⎩⎭



and

max

⎧⎫

⎪⎪

Ω= ≤

⎨⎬

⎪⎪

⎩⎭

In the case where the sliding surface is outside the

region

Ω , for choosing

ρμ

there exists a positive constant

such that:

()

vt s

≤−



(27)

From the definition of the constraint region, we have

()

max

0vV≤ . From the inequality (23), we obtain

()

max

() 0vt v V≤≤ which implies that

s ∈Ω for all

0t ≥ and therefore

e ∈Ω and

e ∈Ω



(Chang-05).

Hence,

CAB

Ω×Ω ×Ω ×Ω is an invariant set, we

can conclude that all the variables are bounded.

Since the Lyapunov function is negative outside the

constraint set

Ω , then sliding surface is Uniformly

Ultimately Bounded (UBB) and hence the tracking

error is also UBB.

By integrating the above inequality between 0 and T,

we obtain:

222

000

() (0)

TTT

vT v dt dt dt

ρδ ρδ

−≤− + +

∫∫∫

222

000

(0) ( )

TTT

dt v v T dt dt

ρδ ρδ

≤−+ +

∫∫∫

(28)

Since

() 0vT ≥ , we have

222

000

TTT

dt dt dt

ρδ ρδ

≤+

∫∫∫

22 22

000

TTT

dt dt dt

ρδ ρδ

≤+

∫

∫∫

(29)

Using the Barbalat’s lemma (Wang, 94), one can see

that the sliding surface converges asymptotically to

zero despite the presence of external disturbances.

Hence, the sliding surface is attractive, i.e., if the

system attains the surface, it remains and converges

toward the origin as demonstrated in (Utkin, 99).

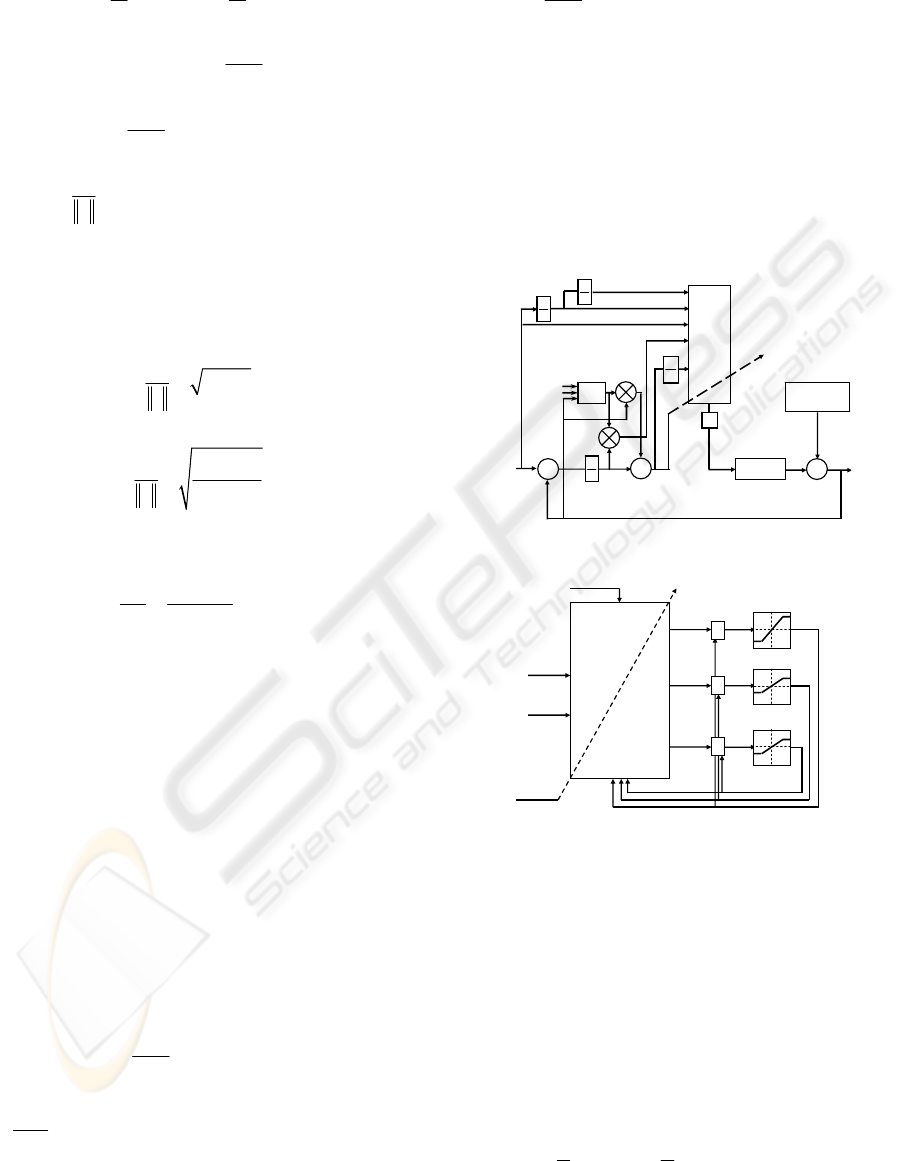
Control

action

synthesis

eq. (14)

Plant

External

disturbance



()dt



()ut



(e)

−

Figure 2: Control scheme of the proposed approach.

AWN

Given in Eq. (4)

Adaptation

Given in Eq.

(20)-(22)

•

∫



CBA

Figure 3: Adaptive Wavelet Network illustration.

5 DESIGN PROCEDURE

The control scheme of the proposed approach and

the adaptive WNN block are given respectively by

figures 2 and 3. The control law (14) can be

synthesised according to the following steps:

Step 1: define the interval range for each input

(, )



and the corresponding wavelet parameters

(dilation and translation) such that input range is

covered uniformly. To adapt on-line the adjustable

parameters

, B and C , we define the learning

ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics

rates

and

. To increase approximator

nonlinearity, we choose

bigger than

and

Step 2: specify the parameters k

and

to calculate

the sliding surface given in (8). To deduce the

control law (14), we choose

. This value represents

a trade-off between the initial starting energy and the

time response in transient state.

Step 3: update the adjustable parameters of the

WNN according to equation (20), (21) and (22).

6 SIMULATION EXAMPLE

In order to validate the proposed controller, the

Wing-Rock Motion (WRM) system is considered in

simulation. Indeed, some combat aircrafts often

operate at subsonic speeds and high angles of attack.

These aircrafts may become unstable due to

oscillation, mainly a rolling motion known as WRM

(Lan, 95) (Lin, 02). the dynamics of WRM system

can be described in a state variable by:

01 2 3 4 5

yb bybybyybyyby

=+ + + + +

    

(30)

Where

y is the roll angle, u is the control action and

d is the external disturbance. The parameters related

( 1,...,5)

bi= are the aerodynamic parameters

given by:

0b = ,

-.01859521b = ,

.015162375b = ,

34 5

.06245153, .00954708 and .02145291.bb b== =

According to the design procedure given in section

5, we will define at first the AWNN. Indeed if we

consider that

cos( )

yt= being the desired reference

trajectory, then the interval range of the desired

output (as well as the actual system output in case of

perfect tracking) will belongs always to the closed

interval [-1, 1]. For the purpose of reliability and to

give some relaxation to our controller, the interval

]5.1,5.1[− is considered as a universe of discourse

for both of input and hidden layers in the WNN

approximator. The number of wavelons (wavelet

neurons) components used in the hidden layer are

four which is enough for covering the interval [-1.5,

1.5] adequately. For a WNN approximator, the

number of waveleons components used in the hidden

layer depends on the network input’s interval and

dynamic complexity for the system to be

approximated. Translation parameters selection is

considered in a way that guarantees the uniform

covering of the [-1.5, 1.5] interval simply using

linspace Matlab

instruction. Dilation parameters

specify the intersection amount between wavelons

activation function (daughter function) which is

chosen to be 0.5 such that the horizontal axes

0.5y

contains these intersection points. The

adjustable parameters

, B and C are initialized to

zero such that random initialization case is avoided

since it doesn’t gives neither same initials nor same

training speed. Alternatively, these parameters might

be chosen through some trials to achieve favourable

transient control performance. For constants

and

corresponding to the learning rates, it is

important to recognize there effects to approximate

accurately the nonlinear system and to avoid

masking nonlinear property in the structure shown in

figure 1. For this, it is better choosing

much

bigger than

and

. In our example, the values

, 0.05

and 0.05

have been

considered. According to the second step in the

design procedure, the variable sliding mode may be

achieved through variation in surface slope

()

. For

this we choose

20k

and 0.5

= .

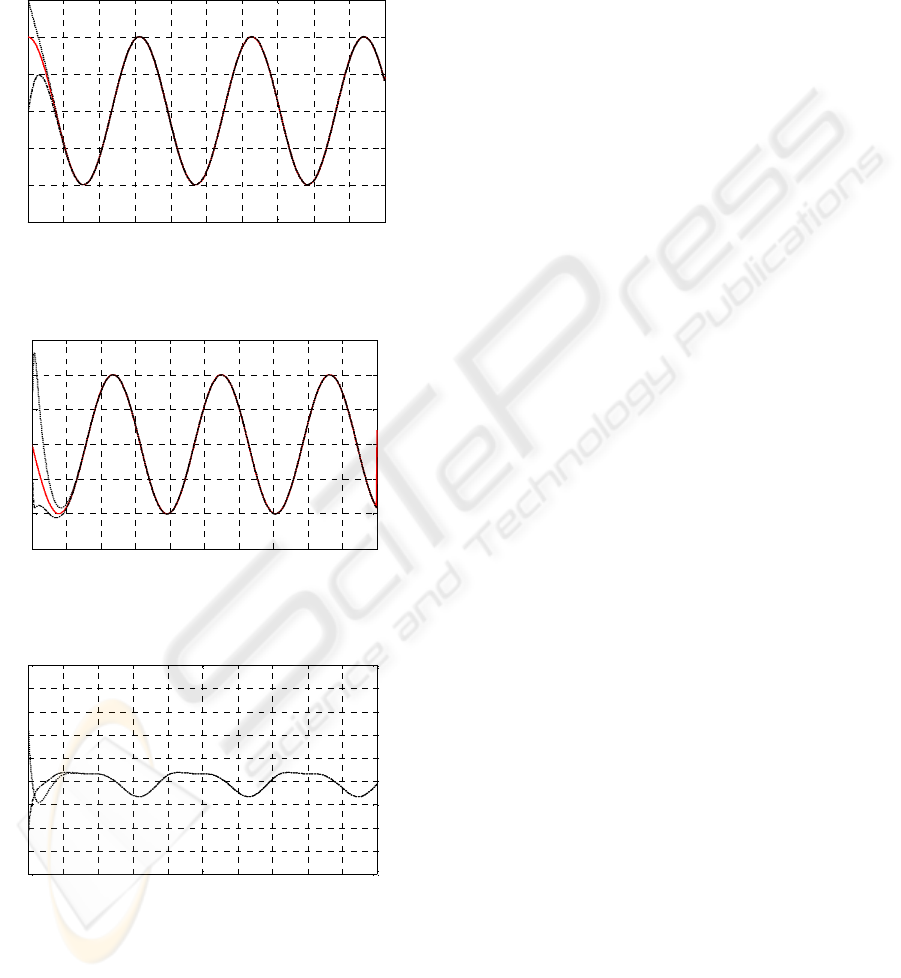
Several simulations have been done and figures 4 to

6 show the results obtained for

0.5

= where the

system is subjected to external disturbance with

0.3sin(2 )dt

. Figures 4 to 6 give the simulation

results for two different initial positions. We remark

that the system attains the reference trajectory

rapidly despite that the initial condition is so far

from the reference one. Short response time reflects

the good convergence of WNN. Furthermore, figure

6 shows the elimination of the chattering

phenomenon and the absence of the abrupt

variations appearing in classical sliding mode

control. Comparing the obtained results with those

in the case of linear sliding surface (

constant), the

proposed approach guarantees the same tracking

performances with 40% initial control action

reduction.

7 CONCLUSION

In this paper a robust adaptive wavelet neural

network to control a class of nonlinear systems was

presented. The combination of WNN and sliding

mode control allows to develop a robust controller to

guarantee the good tracking performances and the

closed loop system stability. Considering a variable

sliding surface reduces the starting energy without

deteriorating the tracking performances.

ROBUST ADAPTIVE WAVELET NEURAL NETWORK TO CONTROL A CLASS OF NONLINEAR SYSTEMS

Furthermore, no knowledge about of the upper

bounds of both the external disturbances and the

approximation errors is required to synthesis the

control law. Simulation results have been presented

to show the efficiency of the proposed approach.

Current work is dedicated to the generalisation of

this method to n

multi-input multi-output systems.

0 2 4 6 8 10 12 14 16 18 2

-1.5

-1

-0.5

0.5

1.5

Time (S)

Figure 4: Evolution of the system output and its reference

signal (-:y

, ..: y(t) with y(0)=1.5; -.-: y(t) with y(0)=0).

0 2 4 6 8 10 12 14 16 18 20

-1.5

-1

-0.5

0.5

1.5

Time (S

)

Figure 5: Evolution of the state



and its reference signal

(-:



, ..:



with y(0)=1.5; -.-:



with y(0)=0).

0 2 4 6 8 10 12 14 16 18 20

-8

-6

-4

-2

Time (S)

Figure 6: The control signal applied to the system (...: u(t)

with y(0)=1.5; -.-: u(t) with y(0)=0).

REFERENCES

Antsaklis, P. J., Jun. 1995. vol. 15, Issue 3, pp. 5 - 7. In

Intelligent Learning Control IEEE Control Syst. Mag.

IEEE Press.

Astrom, K. J., Wittenmark, B., 1995. In Adaptive Control.

Addison-Wesley, 2

edition.

Bartoloni, G., Ferrara, A., Usai, E., 1997. vol. 33 pp.

2203-2212. In Automatica, Output tracking control of

uncertain nonlinear second-order systems. Elsevier.

Berstecher, R.G, Palm, R., Unbehauen, H.D., 2001. vol.

48, pp. 18-31. In An Adaptive Fuzzy Sliding Mode

Controller, IEEE Trans. on Indus. Electr., IEEE press.

Broderick, R. L., 2005. vol. 1, pp. 6.C.2-01-10. In daptive

verification for an on-line learning neural-based flight

control system, the 24th Digital Avionics Systems

Conference, IEEE Press.

Chang, Y. C., Yen, H. M., 2005. vol. 35, pp. 1311-1316.

In Adaptive output Feedback control for a class of

uncertain nonlinear systems using neural networks,

IEEE Trans. Systems, Man, & Cybernetic. IEEE Press.

Chang, Y.-C., 2005. part B: cybernetics

vol. 35, no. 6

pp.1108- 1119. In Intelligent Robust Control for

Uncertain Nonlinear Time-Varying Systems and Its

Application to Robotic Systems, IEEE Trans. on syst.

Man & Cyber., IEEE Press.

Delyon, B., Juditsky, A., Benveniste, A., 1995. vol. 6, no.

2, pp.332–348. In Accuracy analysis for wavelet

approximations, IEEE Trans. Neural Networks. IEEE

Press.

Fabri, S., Kadirkamanathan, V., Sept. 1996. vol. 7, pp.

1151–1167, Dynamic structure neural networks for

stable adaptive control of nonlinear systems, IEEE

Trans. Neural Networks IEEE press.

Farrell, J., Baker, W., 1993. pp. 237-262. In Learning

control systems, In Passino, K. M., Antsaklis, P. J.

(Eds.), An Introduction to Intelligent and Autonomous

Control. Kluwer Academic Publishers.

Farrell, J. A., Sept. 1998. vol. 9, pp.1008–1020 Stability

and approximator convergence in nonparametric

nonlinear adaptive control,” IEEE Trans. Neural

Networks. IEEE press.

Grman, J., Ravas, R., Syrová, L., 2001. vol. 1, no. 1, pp.

25–28. In Application of Neural Networks in

Multifrequency Eddy-Current Testing, Measurement

Science Review. Slovak Academy of Sciences.

Hamzaoui, A., Essounbouli, N., Zaytoon, J., 2004. vol.

218 (4), pp. 287-298. In Fuzzy sliding mode control

with fuzzy switching function for nonlinear uncertain

MIMO Systems, Journal of Systems and Control

Engineering.

Ho, D. W. C., Li, J., Niu, Y., 2005. vol. 16, no. 3, pp. 625-

635. Adaptive Neural Control for a Class of

Nonlinearly Parametric Time-Delay Systems, IEEE

Trans. on Neural Networks, IEEE Press.

Hsu, C.F., Lin, C.M., Lee, T.T., 2006. vol. 17, no. 5, pp.

1175-1183. In Wavelet Adaptive Backstepping Control

ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics

for a Class of Nonlinear Systems, IEEE Trans. On

Neural Networks, IEEE Press.

Huang, S. N., Tan, K. K,. Lee, T. H., 2002. vol. 38, no. 2,

pp. 227–233. In Automatica, Adaptive motion control

using neural network approximations, Elsevier.

Hwang, C.-L., Kuo, C.-Y., 2001. vol. 9 (2), pp. 238-252.

In A stable adaptive fuzzy sliding-mode control for

affine nonlinear systems with application to four-bar

linkage systems, IEEE Trans. On Fuzzy Syst. IEEE

press.

Kostka, P., Tkacz, E. J., Nawrat, Z., Malota, Z., 2000. pp.

2463-2465. In An application of wavelet neural

networks for heart valve prostheses characteristic,

Proceedings of the 22nd Annual EMBS International

Conference, IEEE Press.

Lan, C. E., Chen, Y., Lin, K. J., 1995. vol. 32, pp. 905–

910. In Experimental and analytical investigations of

transonic limit-cycle oscillations of a flaperon,

Journal Aircraft, American Institute of Aeronautics

and Astronautics.

Lin, C. M., Hsu, C. F., 2002. vol. 25, pp. 1163–1165,2002.

In Recurrent neural network adaptive control of wing

rock motion, Journal of guidance, control, and

dynamics. American Institute of Aeronautics and

Astronautics.

Lin, S.C., Chen, Y.Y., Mar. 1995. vol. 3, pp. 1103-1110.

In A GA-based fuzzy controller with sliding mode,

Proc. IEEE Int.Conf. on Fuzzy Systems. IEEE Press.

Lin, F. J., Hwang, W. J., Wai, R. J., 1998. vol. 145, no. 2,

pp. 105–110, Ultrasonic motor servo drive with on-

line trained neural network model-following

controller, Proc.IEE—Elect. Power Applicat. . IEEE

press.

Lin, W.-S., Chen, C.-S., 2002. vol. 149, pp. 193-202. In

Robust adaptive sliding mode control using fuzzy

modelling for a class of uncertain MIMO nonlinear

systems, IEE Proceedings: Control Theory and

Applications, IEEE Press.

Lin, F.J., Wai, R. J., Chen, M. P., 2003. vol. 20, no. 6, pp.

686-698. In Wavelet Neural Network Control for

Linear Ultrasonic Motor Drive via Adaptive Sliding-

Mode Technique, IEEE Trans. On Ultrasonics,

Ferroelectrics & Frequency Control, IEEE Press.

Liu, Z. L., Nov. 2005. vol. 152, no. 6, pp. 615- 620

Reinforcement adaptive fuzzy control of wing rock

phenomena, IEE proc. Control theory appl. IEE press.

Narendra, K. S., Parthasarathy, K., Mar. 1990. vol. 1, no.

1, pp. 4–27, 1990. In Identification and control of

dynamic systems using neural networks, IEEE Trans.

Neural Net. IEEE press.

Noriega, J. R., Wang, H, Jan. 1998. vol. 9, pp. 27–34.

direct adaptive neural-network control for unknown

nonlinear systems and its application, IEEE Trans.

Neural Network, IEEE Press.Omidvar, O., Elliott, D.

L., 1997. Neural Systems for Control. New York:

Academic.

Omidvar, O., Elliott, D. L., 1997. Neural Systems for

Control. New York: Academic.

Oussar, Y., Rivals, I., Personnaz, L., Dreyfus, G., 1998.

vol. 20, pp. 173-188, 1998. In Training wavelet

networks for nonlinear dynamic input-output

modeling, Neurocomputing, Elsevier

Psillakis, H. E., Alexandridis, A. T., Mar. 2006. vol. 153,

No. 2. In Adaptive neural motion control of n-link

robot manipulators subject to unknown disturbances

and stochastic perturbations. IEE Proc. Control

Theory Appl. IEE press.

Roup, A. V., Bernstein, D. S., 2001. vol. 46, pp. 1821-

1825. In Adaptive stabilization of a class of non-linear

systems with parametric uncertainties, IEEE Trans.

Automatic Control, IEEE Press.

Salamci, M. U., Ozgoren, M. K., 2001. vol. 23, no. 4, pp.

719-727. Sliding mode control with optimal sliding

surfaces for missile autopilot design, Journal of

Guidance, Control and Dynamics, , 2001.

Sastry, S., Bodson, M., 1989. In Adaptive Control:

Stability, Convergence, and Robustness. Prentice-Hall.

Seshagiri, S., Khalil, H. K., Jan. 2000. vol. 11, pp. 69–79,

Output feedback control of nonlinear systems using

RBF neural network,” IEEE Trans. Neural Networks

IEEE press.

Slotine, J.-J. E., Li, W., 1991. In Applied Nonlinear

Control. Prentice-Hall.

Sureshbabu, N., Farrell, J. A., Feb. 1999. vol. 44, no. 2,

pp.412-417. In Wavelet-Based System Identification

for Nonlinear Control, IEEE Transactions on

automatic control,IEEE Press.

Utkin, V.I., 1977. vol. 22, pp. 212-222.Variable structure

systems with sliding modes,” IEEE Trans. Automatic

Control, IEEE Press.

Utkin, V. I., 1999. vol. 22, pp. 212-222. In Variable

structure systems with sliding modes, IEEE Trans.

Automatic Control, IEEE Press.

Wai, R.J., Lin, C. M., Hsu, C.F., 2004. vol. 143, pp. 295-

310. In Adaptive fuzzy sliding mode control for

electrical servo drive, Fuzzy Sets & Systems, Elsevier.

Wang, L.-X., 1994. In Adaptive fuzzy systems and control,

Prentice-Hall.

Wong, L.K., Leung, F.H.F., Tam, P.K.S., 1998. vol. 1, pp.

296-301. In Combination of sliding mode controller

and PI controller Using fuzzy logic controller,

IEEE

Int. Conf. on Fuzzy Systems. IEEE Press.

Yoo, S. J., Park, J. B., Choi, Y. H. Mar. 2005. vol. 3, no.

1, pp. 43–55. In Stable Predictive Control of Chaotic

Systems Using Self-Recurrent Wavelet Neural

Network, International Journal of Control,

Automation, and Systems, IEEE Press.

Zhang, Q., Walter, G. G., Miao, Y., Lee, W. N. W., Jun.

1995. vol. 43, pp. 1485-1496. In Wavelet neural

networks for function learning, IEEE Trans. Signal

Proc., IEEE Press.

ROBUST ADAPTIVE WAVELET NEURAL NETWORK TO CONTROL A CLASS OF NONLINEAR SYSTEMS