RSRT: RAPIDLY EXPLORING SORTED RANDOM TREE
Online Adapting RRT to Reduce Computational Solving Time
while Motion Planning in Wide Configuration Spaces
Nicolas Jouandeau
L.I.A.S.D.
Dept. MIME
Université Paris8
Keywords:
Motion-planning, soft computing.
Abstract:
We present a new algorithm, named RSRT, for Rapidly-exploring Random Trees (RRT) based on inherent
relations analysis between RRT components. RRT algorithms are designed to consider interactions between
these inherent components. We explain properties of known variations and we present some future once which
are required to deal with dynamic strategies. We present experimental results for a wide set of path planning
problems involving a free flying object in a static environment. The results show that our RSRT algorithm
(where RSRT stands for Rapidly-exploring Sorted Random Trees) is faster than existing ones. This results
can also stand as a starting point of a motion planning benchmark instances which would make easier further
comparative studies of path planning algorithms.
1 INTRODUCTION
Literally, planning is the definition of a sequence of
orders which reach a previously selected goal. In a ge-
ometrical context, planning considers a workspace, an
initial position, a final position and a set of constraints
characterizing a mobile M. The problem of planning
could be resumed in two questions: the existence of
a solution to a given problem and the definition of a
solution to a problem that has at least one solution.
In this paper, the problem of planning is focused on
the second one, i.e. identifying solutions for problems
that have at least one solution. The complexity of such
a solution depends on the mobile workspace, its car-
acteristics (i.e. number of degrees of freedom) and the
required answer complexity (i.e. the model and the
local planner). Each dimension of these three parts
contributes to define the problem dimension. Com-
plexity is exponential in the problem dimension, so
probabilistic methods propose to solve geometrical
path-planning problems by finding a valid solution
without guarantee of optimality. This particular re-
lation to optimality associates probabilistic methods
with problems known as difficult (also called non-
deterministic polynomial in space (Canny, 1987)). In
these methods, solving a path-planning problem con-
sists in exploring the space in order to compute a so-
lution with a determinist algorithm (Latombe, 1991).
The specificity of these methods can be summarized
with a random sampling of the search space, which
reduces the determinist-polynomial complexity of the
resolution (Schwartz and Sharir, 1983). The increase
of computers capacities and the progress of the proba-
bilistic methods, made solvable problems more com-
plex during last decades. The principal alternatives of
research space are the configuration spaceC (Lozano-
Pérez, 1983), the state space X (Donald et al., 1993)
and the state-time space ST (Fraichard, 1993). C is
intended to motion planning in static environments.
X adds differential constraints. ST adds the possi-
bility of a dynamic environment. The concept of
high-dimensional configuration spaces is initiated by
J. Barraquand et al. (Barraquand and Latombe, 1990)
to use a manipulator with 31 degrees of freedom. P.
Cheng (Cheng, 2001) uses these methods with a 12
dimensional state space involving rotating rigid ob-
jects in 3D space. S. M. LaValle (LaValle, 2004)
presents such a space with a hundred dimensions for
either a robot manipulator or a couple of mobiles.
The probabilistic methods mostly used in such spaces
are Randomized Path Planning (RPP), Probabilis-
tic RoadMap (PRM) and Rapidly exploring Random
100
Jouandeau N. (2007).
RSRT: RAPIDLY EXPLORING SORTED RANDOM TREE - Online Adapting RRT to Reduce Computational Solving Time while Motion Planning in Wide
Configuration Spaces.
In Proceedings of the Fourth International Conference on Informatics in Control, Automation and Robotics, pages 100-107
DOI: 10.5220/0001622001000107
Copyright
c
 SciTePress

Trees (RRT). The RPP method introduced by J. Bar-
raquand et al. (Barraquand and Latombe, 1991) is a
variation of the gradient method also introduced by
O. Khatib (Khatib, 1985). Random moves make pos-
sible to escape from the local minima and recover the
completeness. These random moves follow a Gaus-
sian law. Each move is independent of the previous
one. With obstacles, moves must remain in free space
C
free
. In case of collision, moves are reflected on the
obstacles. The PRM method is introduced simulta-
neously by L.E. Kavraki et al. (Kavraki, 1995) and
by P. Svestka et al. (Svestka, 1997) under the head-
ing Probabilistic Path Planner (PPP). Their resolu-
tion principle divides the path planning problem into
two successive stages: a learning phase that builds a
graph and a query phase that builds a solution based
on the previous graph. During the learning phase,
the graph is built in C
free
where each node is ran-
domly selected according to a uniform distribution in
C
free
. This uniform distribution is justified by the
need of exploring the entire free space. It is ob-
tained by a random sampling associated to a colli-
sion detector. During the query phase, the graph
is used to connect two configurations q
init
and q
obj
included in C
free
. At each iteration, a local path
planner seeks a way to connect a new node to the
graph and also tries to connect q
init
and q
obj
. The
RRT method introduced by S.M. LaValle (LaValle,
1998) is based on the construction of a tree T in the
considered space
S . Starting from the initial position
q
init
, the construction of the tree is carried out by inte-
grating control commands iteratively. Each iteration
aims at bringing closer the mobile M to an element
e randomly selected in
S . To avoid cycles, two ele-
ments e of T cannot be identical. In practice, RRT
is used to solve various problems such as negotiating
narrow passages made of obstacles (Ferré and Lau-
mond, 2004), finding motions that satisfy obstacle-
avoidance and dynamic balances constraints (Kuffner
et al., 2003), making Mars exploration vehicles strate-
gies (Williams et al., ), searching hidden objects (To-
var et al., 2003), rallying a set of points or play-
ing hide-and-seek with another mobile (Simov et al.,
2002) and many others mentioned in (LaValle, 2004).
Thus by their efficiency to solve a large set of prob-
lems, the RRT method can be considered as the most
general one.
In the next section, we present existing RRT algo-
rithms.
2 RAPIDLY EXPLORING
RANDOM TREES
In its initial formulation, RRT algorithms are de-
fined without goal. The exploration tree covers the
surrounding space and progress blindly towards free
space.
A geometrical path planning problem aims gener-
ally at joining a final configuration q
obj
. To solve the
path planning problem, the RRT method searches a
solution by building a tree (ALG. 1) rooted at the ini-
tial configuration q
init
. Each node of the tree results
from the mobile constraints integration. Its edges are
commands that are applied to move the mobile from
a configuration to another.
The RRT method is a random incremental search
which could be casting in the same framework of
Las Vegas Algorithms (LVA). It repeats successively a
loop made of three phases: generating a random con-
figuration q
rand
, selecting the nearest configuration
q
prox
, generating a new configuration q
new
obtained
by numerical integration over a fixed time step ∆t.
The mobile M and its constraints are not explic-
itly specified. Therefore, modifications for additional
constraints (such as non-holonomic) are considered
minor in the algorithm formulation.
In this first version, C is presented without obsta-
cle in an arbitrary space dimension. At each itera-
tion, a local planner is used to connect each couples
(q
new
, q
prox
) in C. The distance between two configu-
rations in T is defined by the time-step ∆t. The local
planner is composed by temporal and geometrical in-
tegration constraints. The resulting solution accuracy
is mainly due to the chosen local planner. k defines
the maximum depth of the search. If no solution is
found after k iterations, the search can be restarted
with the previous T without re-executing the init func-
tion (ALG. 1 line 1).
The RRT method, inspired by traditional Artifi-
cial Intelligent techniques for finding sequences be-
tween an initial and a final element (i.e. q
init
and
q
obj
) in a well-known environment, can become a
bidirectional search (shortened Bi-RRT (LaValle and
Kuffner, 1999)). Its principle is based on the simulta-
neous construction of two trees (called T
init
and T
obj
)
in which the first grows from q
init
and the second
from q
obj
. The two trees are developped towards
each other while no connection is established between
them. This bidirectional search is justified because
the meeting configuration of the two trees is nearly
the half-course of the configuration space separating
q
init
and q
obj
. Therefore, the resolution time complex-
ity is reduced (Russell and Norvig, 2003).
RSRT: RAPIDLY EXPLORING SORTED RANDOM TREE - Online Adapting RRT to Reduce Computational Solving
Time while Motion Planning in Wide Configuration Spaces
101

rrt(q
init
, k, ∆t,C)
1 init(q
init
, T);
2 for i ← 1 à k
3
q
rand
← randomState(C);
4
q
prox
← nearbyState(q
rand
, T);
5
q
new
← newState(q
prox
, q
rand
, ∆t);
6
addState(q
new
, T);
7
addLink(q
prox
, q
new
, T);
8 return T;
ALG. 1: Basic RRT building algorithm.
RRT-Connect (Kuffner and LaValle, 2000) is a
variation of Bi-RRT that consequently increase the Bi-
RRT convergence towards a solution thanks to the en-
hancement of the two trees convergence. This has
been settled to:
• ensure a fast resolution for “simple” problems (in
a space without obstacle, the RRT growth should
be faster than in a space with many obstacles);
• maintain the probabilistic convergence property.
Using heuristics modify the probability conver-
gence towards the goal and also should modify
its evolving distribution. Modifying the random
sampling can create local minima that could slow
down the algorithm convergence.
connectT(q, ∆t, T)
1 r ← ADVANCED;
2 while r = ADVANCED
3
r ← expandT(q, ∆t, T);
4 return r;
ALG. 2: Connecting a configuration q to a graph T with
RRT-Connect.
In RRT-Connect, the two graphs previously called
T
init
and T
obj
are called now T
a
and T
b
(ALG. 3). T
a
(respectively T
b
) replaces T
init
and T
obj
alternatively
(respectively T
obj
and T
init
). The main contribution of
RRT-Connect is the ConnectT function which move
towards the same configuration as long as possible
(i.e. without collision). As the incremental nature al-
gorithm is reduced, this variation is designed for non-
differential constraints. This is iteratively realized by
the expansion function (ALG. 2). A connection is de-
fined as a succession of successful extensions. An ex-
pansion towards a configuration q becomes either an
extension or a connection. After connecting success-
fully q
new
to T
a
, the algorithm tries as many exten-
sions as possible towards q
new
to T
b
. The configura-
tion q
new
becomes the convergence configuration q
co
(ALG. 3 lines 8 and 10).
rrtConnect(q
init
, q
obj
, k, ∆t,C)
1 init(q
init
, T
a
);
2 init(q
obj
, T
b
);
3 for i ← 1 à k
4
q
rand
← randomState(C);
5
r ← expandT(q
rand
, ∆t, T
a
);
6
if r 6= TRAPPED
7 if r = REACHED
8 q
co
← q
rand
;
9 else
10
q
co
← q
new
;
11 if connectT(q
co
, ∆t, T
b
) =
REACHED
12
sol ← plan(q
co
, T
a
, T
b
);
13
return sol;
14
swapT(T
a
, T
b
);
15 return TRAPPED;
ALG. 3: Expanding two graphs T
a
and T
b
towards them-
selves with RRT-Connect. q
new
mentionned line 10 cor-
reponds to the q
new
variable mentionned line 9 ALG. 4.
Inherent relations inside the adequate construction
of T in C
free
shown in previous works are:
• the deviation of random sampling in the varia-
tions Bi-RRT and RRT-Connect. Variations in-
clude in RRT-Connect are called RRT-ExtCon,
RRT-ConCon and RRT-ExtExt; they modify the
construction strategy of one of the two trees of
the method RRT-Connect by changing priorities
of the extension and connection phases (LaValle
and Kuffner, 2000).
• the well-adapted q
prox
element selected according
to its collision probability in the variation CVP
and the integration of collision detection since
q
prox
generation (Cheng and LaValle, 2001).
• the adaptation of C to the vicinity accessibil-
ity of q
prox
in the variation RC-RRT (Cheng and
LaValle, 2002).
• the parallel execution of growing operations for
n distinct graphs in the variation OR parallel Bi-
RRT and the growing of a shared graph with a
parallel q
new
sampling in the variation embarrass-
ingly parallel Bi-RRT (Carpin and Pagello, 2002).
• the sampling adaptation to the RRT
ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics
102

growth (Jouandeau and Chérif, 2004; Cortès
and Siméon, 2004; Lindemann and LaValle,
2003; Lindemann and LaValle, 2004; Yershova
et al., 2005).
By adding the collision detection in the given
space S during the expansion phase, the selection
of nearest neighbor q
prox
is realized in S ∩ C
free
(ALG. 4). Although the collision detection is expen-
sive in computing time, the distance metric evaluation
ρ is subordinate to the collision detector. U defines
the set of admissible orders available to the mobile M.
For each expansion, the function expandT (ALG. 4)
returns three possible values: REACHED if the con-
figuration q
new
is connected to T, ADVANCED if q
is only an extension of q
new
which is not connected
to T, and TRAPPED if q cannot accept any successor
configuration q
new
.
expandT(q,∆t, T)
1 q
prox
← nearbyState(q, T);
2 d
min
← ρ(q
prox
, q);
3 success ← FALSE;
4 foreach u ∈ U
5
q
tmp
← integrate(q, u, ∆t);
6
if isCollisionFree(q
tmp
, q
prox
, M,C)
7 d ← ρ(q
tmp
, q
rand
);
8 if d < d
min
9
q
new
← q
tmp
;
10
d
min
← d;
11
success ← TRUE;
12 if success = TRUE
13 insertState(q
prox
, q
new
, T);
14
if q
new
= q
15 return REACHED;
14 return ADVANCED;
17 return TRAPPED;
ALG. 4: Expanding T with obstacles.
In the next section, we examine in detail justifi-
cations of our algorithm and the inherent relations in
the various components used. This study enables us to
synthesize a new algorithm named Rapidly exploring
Sorted Random Tree (RSRT), based on reducing col-
lision detector calls without modification of the clas-
sical random sampling strategy.
3 RSRT ALGORITHM
Variations of RRT method presented in the previous
section is based on the following sequence :
• generating q
rand
;
• selecting q
prox
in T;
• generating each successor of q
prox
defined in U.
• realizing a colliding test for each successor previ-
ously defined;
• selecting a configuration called q
new
that is the
closest to q
rand
among successors previously de-
fined; This selected configuration has to be colli-
sion free.
The construction of T corresponds to the repeti-
tion of such a sequence. The collision detection dis-
criminates the two possible results of each sequence:
• the insertion of q
new
in T (i.e. without obstacle
along the path between q
prox
and q
new
);
• the rejection of each q
prox
successors (i.e. due to
the presence of at least one obstacle along each
successors path rooted at q
prox
).
The rejection of q
new
induces an expansion prob-
ability related to its vicinity (and then also to q
prox
vicinity); the more the configuration q
prox
is close to
obstacles, the more its expansion probability is weak.
It reminds one of fundamentals RRT paradigm: free
spaces are made of configurations that admit various
number of available successors; good configurations
admit many successors and bad configurations admit
only few ones. Therefore, the more good configu-
rations are inserted in T, the better the RRT expan-
sion will be. The problem is that we do not previ-
ously know which good and bad configurations are
needed during RRT construction, because the solu-
tion of the considered problem is not yet known. This
problem is also underlined by the parallel variation
OR Bi-RRT (Carpin and Pagello, 2002) (i.e. to de-
fine the depth of a search in a specific vicinity). For
a path planning problem p with a solution s avail-
able after n integrations starting from q
init
, the ques-
tion is to maximize the probability of finding a solu-
tion; According to the concept of “rational action”,
the response of P3 class to adapt a on-line search can
be solved by the definition of a formula that defines
the cost of the search in terms of “local effects” and
“propagations” (Russell, 2002). These problems find
a way in the tuning of the behavior algorithm like
CVP did (Cheng and LaValle, 2001).
In the case of a space made of a single narrow pas-
sage, the use of bad configurations (which successors
RSRT: RAPIDLY EXPLORING SORTED RANDOM TREE - Online Adapting RRT to Reduce Computational Solving
Time while Motion Planning in Wide Configuration Spaces
103

generally collide) is necessary to resolve such prob-
lem. The weak probability of such configurations ex-
tension is one of the weakness of the RRT method.
newExpandT(q, ∆t, T)
1 q
prox
← nearbyState(q, T);
2 S ←
/
0;
3 foreach u ∈ U
4
q ← integrate(q
prox
, u, ∆t);
5
d ← ρ(q, q
rand
);
6
S ← S+ {(q, d)};
7 qsort(S, d);
8 n ← 0;
10 while n < Card(S)
11
s ← getTupleIn(n, S);
12
q
new
← firstElementOf(s);
13
if isCollisionFree(q
new
, q
prox
, M,C)
14 insertState(q
prox
, q
new
, T);
15 if q
new
= q
16
return REACHED;
17 return ADVANCED;
18
n ← n+ 1;
19 return TRAPPED;
ALG. 5: Expanding T and reducing the collision detec-
tion.
To bypass this weakness, we propose to reduce re-
search from the closest element (ALG. 4) to the first
free element ofC
free
. This is realized by reversing the
relation between collision detection and distance met-
ric; the solution of each iteration is validated by sub-
ordinating collision tests to the distance metric; the
first success call to the collision detector validates a
solution. This inversion induces:
• a reduction of the number of calls to the collision
detector proportionally to the nature and the di-
mension of U; Its goal is to connect the collision
detector and the derivative function that produce
each q
prox
successor.
• an equiprobability expansion of each node inde-
pendently of their relationship with obstacles;
The T construction is now based on the following
sequence:
1. generating a random configuration q
rand
in C;
2. selecting q
prox
the nearest configuration to q
rand
in T (ALG. 5 line 1);
3. generating each successors of q
prox
(ALG. 5
lines 3 to 6); each successor is associated with its
distance metric from q
rand
. It produces a couple
called s stored in S;
4. sorting s elements by distance (ALG. 5 lines 7);
5. selecting the first collision-free element of S and
breaking the loop as soon as this first element is
discovered (ALG. 5 lines 16 and 17);
4 EXPERIMENTS
This section presents experiments performed on a
Redhat Linux Cluster that consists of 8 Dual Core
processor 2.8 GHz Pentium 4 (5583 bogomips) with
512 MB DDR Ram.
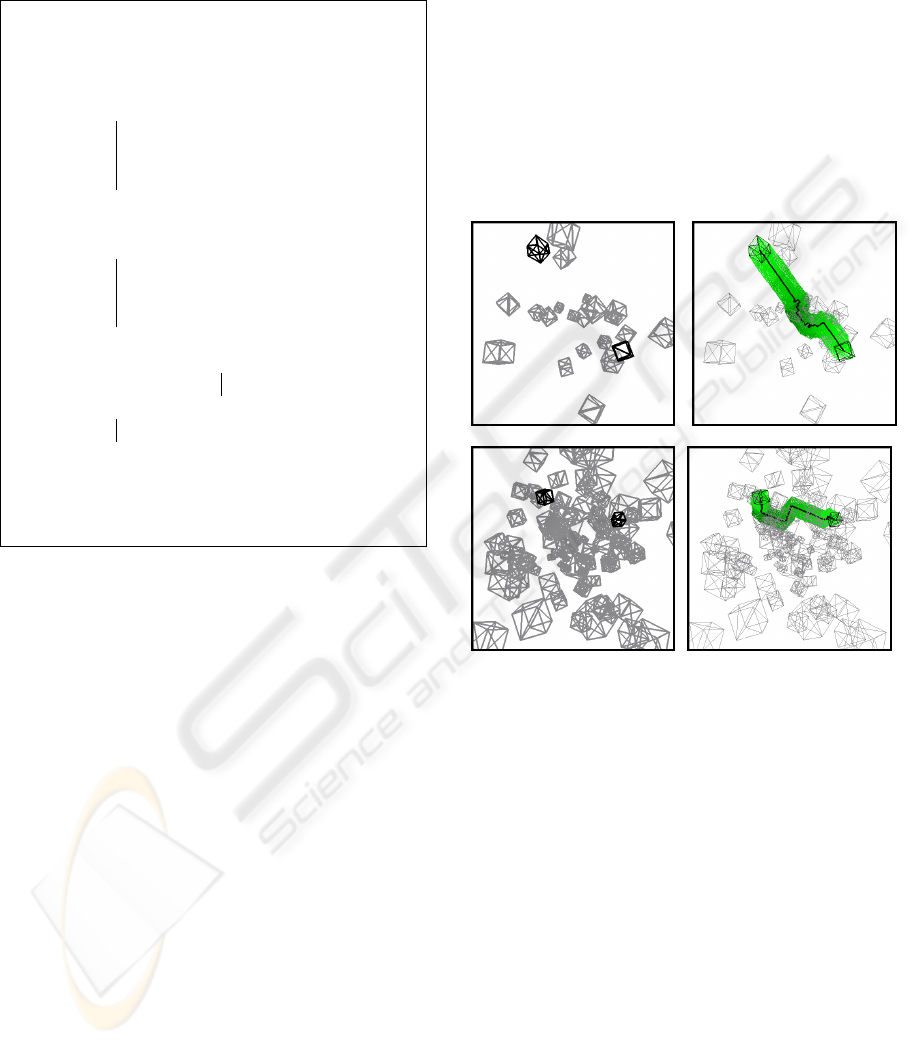
Figure 1: 20 obstacles problem and its solution (upper cou-
ple). 100 obstacles problem and its solution (lower couple).
To perform the run-time behavior analysis for our
algorithm, we have generated series of problems that
gradually contains more 3D-obstacles. For each prob-
lem, we have randomly generated ten different in-
stances. The number of obstacles is defined by the
sequence 20, 40, 60, . . . , 200, 220. In each instance,
all obstacles are cubes and their sizes are randomly
varying between (5, 5, 5) and (20, 20, 20). The mo-
bile is a cube with a fixed size (10, 10, 10). Ob-
stacles and mobile coordinates are varying between
(−100, −100, −100) and (100, 100, 100). For each
instance, a set of 120 q
init
and 120 q
obj
are gener-
ated inC
free
. By combinating each q
init
and each q
obj
,
14400 configuration-tuples are available for each in-
stance of each problem. For all that, our benchmark is
made of more than 1.5 million problems. An instance
with 20 obstacles is shown in FIG. 1 on the lower
part and another instance with 100 obstacles in FIG. 1
ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics
104

on the left part. On these two examples, q
init
and
q
obj
are also visible. We used the Proximity Query
Package (PQP) library presented in (Gottschalk et al.,
1996) to perform the collision detection. The mo-
bile is a free-flying object controlled by a discretized
command that contains 25 different inputs uniformly
dispatched over translations and rotations. The per-
formance was compared between RRT-Connect (us-
ing the RRT-ExtCon strategy) and our RSRT algorithm
(ALG. 5).
The choice of the distance metric implies im-
portant consequences on configurations’ connexity in
C
free
. It defines the next convergence node q
co
for the
local planner. The metric distance must be selected
according to the behavior of the local planner to limit
its failures. The local planner chosen is the straight
line in C. To validate the toughness of our algorithm
regarding to RRT-Connect, we had use three different
distance metrics. Used distance metrics are:
• the Euclidean distance (mentioned Eucl in
FIG. 2 to 4)
d(q, q
′
) =
i
∑
k=0
(c
k
− c
′
k
)
2
+ nf
2
j
∑
k=0
(α
k
− α
′
k
)
2
!
1
2
where nf is the normalization factor that is equal
to the maximum of c
k
range values.
• the scaled Euclidean distance metric (mentioned
Eucl2 in FIG. 2 to 4)
d(q, q
′
) = s
i
∑
k=0
(c
k
− c
′
k
)
2
+ nf
2
(1− s)
j
∑
k=0
(α
k
− α
′
k
)
2
!
1
2
where s is a fixed value 0.9;
• the Manhattan distance metric (mentioned Manh
in FIG. 2 to 4)
d(q, q
′
) =
i
∑
k=0
kc
k
− c
′
k
k + nf
j
∑
k=0
kα
k
− α
′
k
k
where c
k
are axis coordinates and α
k
are angular
coordinates.
For each instance, we compute the first thou-
sand successful trials to establish average resolv-
ing times (FIG. 2), standard deviation resolving
times (FIG. 3) and midpoint resolving times (FIG. 4).
These trials are initiated with a fixed random set of
seed. Those fixed seed assume that tested random
suite are different between each other and are the
same between instances of all problems. As each in-
stance is associated to one thousand trials, each point
of each graph is the average over ten instances (and
then over ten thousands trials).
0
5
10
15
20
25
0 50 100 150 200
Rrt with Eucl
Rrt with Eucl2
Rrt with Manh
new Rrt with Eucl
new Rrt with Eucl2
new Rrt with Manh
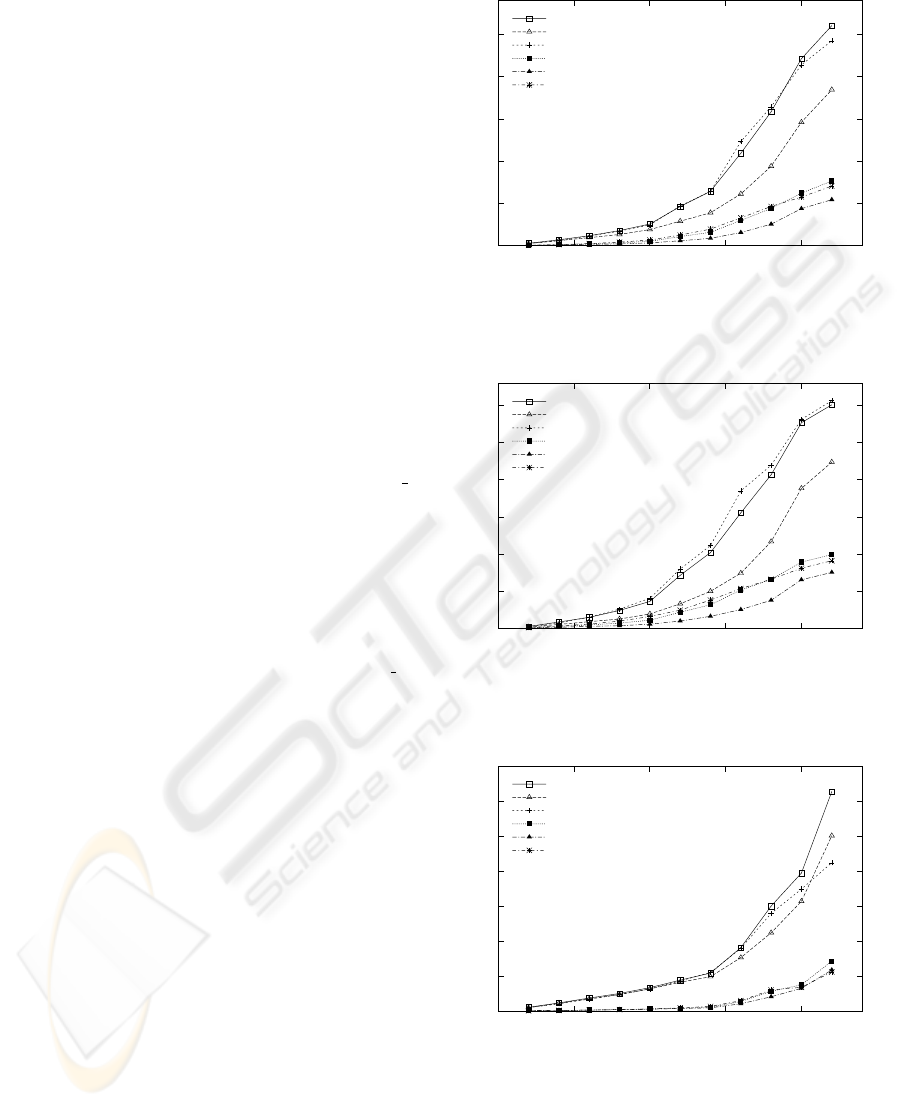
Figure 2: Averages resolving times.
0
5
10
15
20
25
30
0 50 100 150 200
Rrt with Eucl
Rrt with Eucl2
Rrt with Manh
new Rrt with Eucl
new Rrt with Eucl2
new Rrt with Manh
Figure 3: Standard deviation resolving times.
0
2
4
6
8
10
12
14
0 50 100 150 200
Rrt with Eucl
Rrt with Eucl2
Rrt with Manh
new Rrt with Eucl
new Rrt with Eucl2
new Rrt with Manh
Figure 4: Midpoint resolving times.
On each graph, the number of obstacles is on x-axis
and resolving time in sec. is on y-axis.
Figure 2 shows that average resolving time of our
algorithm oscillates between 10 and 4 times faster
RSRT: RAPIDLY EXPLORING SORTED RANDOM TREE - Online Adapting RRT to Reduce Computational Solving
Time while Motion Planning in Wide Configuration Spaces
105

than the original RRT-Connect algorithm. As the
space obstruction grows linearly, the resolving time of
RRT-Connect grows exponentially while RSRT algo-
rithm grows linearly. Figure 3 shows that the standard
deviation follows the same profile. It shows that RSRT
algorithm is more robust than RRT-Connect. Figure 4
shows that midpoints’ distributions follow the aver-
age resolving time behavior. This is a reinforcement
of the success of the RSRT algorithm. This assumes
that half part of time distribution are 10 to 4 times
faster than RRT-Connect.
5 CONCLUSION
We have described a new RRT algorithm, the RSRT al-
gorithm, to solve motion planning problems in static
environments. RSRT algorithm accelerates conse-
quently the resulting resolving time. The experiments
show the practical performances of the RSRT algo-
rithm, and the results reflect its classical behavior.
The results given above( have been evaluated on a
cluster which provide a massive experiment analysis.
The challenging goal is now to extend the benchmark
that is proposed to every motion planning methods.
The proposed benchmark will be enhanced to specific
situations that allow RRT to deal with motion plan-
ning strategies based on statistical analysis.
REFERENCES
Barraquand, J. and Latombe, J. (1990). A Monte-Carlo
Algorithm for Path Planning with many degrees of
Freedom. In Int. Conf. on Robotics and Automation
(ICRA’90).
Barraquand, J. and Latombe, J. (1991). Robot motion plan-
ning: A distributed representation approach. Int. Jour-
nal of Robotics Research (IJRR’91).
Canny, J. (1987). The complexity of robot motion plan-
ning. PhD thesis, Massachusetts Institute of Technol-
ogy. Artificial Intelligence Laboratory.
Carpin, S. and Pagello, E. (2002). On Parallel RRTs for
Multi-robot Systems. In 8th Conf. of the Italian Asso-
ciation for Artificial Intelligence (AI*IA’02).
Cheng, P. (2001). Reducing rrt metric sensitivity for motion
planning with differential constraints. Master’s thesis,
Iowa State University.
Cheng, P. and LaValle, S. (2001). Reducing Metric Sensi-
tivity in Randomized Trajectory Design. In Int. Conf.
on Intelligent Robots and Systems (IROS’01).
Cheng, P. and LaValle, S. (2002). Resolution Complete
Rapidly-Exploring Random Trees. In Int. Conf. on
Robotics and Automation (ICRA’02).
Cortès, J. and Siméon, T. (2004). Sampling-based motion
planning under kinematic loop-closure constraints. In
Workshop on the Algorithmic Foundations of Robotics
(WAFR’04).
Donald, B., Xavier, P., Canny, J., and Reif, J. (1993). Kino-
dynamic Motion Planning. Journal of the ACM.
Ferré, E. and Laumond, J. (2004). An iterative diffusion
algorithm for part disassembly. In Int. Conf. Robotics
and Automation (ICRA’04).
Fraichard, T. (1993). Dynamic trajectory planning with dy-
namic constraints: a "state-time space" approach. In
Int. Conf. Robotics and Automation (ICRA’93).
Gottschalk, S., Lin, M., and Manocha, D. (1996). Obb-tree:
A hierarchical structure for rapid interference detec-
tion. In Proc. of ACM Siggraph’96.
Jouandeau, N. and Chérif, A. A. (2004). Fast Approxima-
tion to gaussian random sampling for randomized mo-
tion planning. In Int. Symp. on Intelligent Autonomous
Vehicules (IAV’04).
Kavraki, L. (1995). Random networks in configuration
space for fast path planning. PhD thesis, Stanford
University.
Khatib, O. (1985). Real-time obstacle avoidance for manip-
ulators and mobile robots. In Int. Conf. on Robotics
and Automation (ICRA’85).
Kuffner, J. and LaValle, S. (2000). RRT-Connect: An effi-
cient approach to single-query path planning. In Int.
Conf. on Robotics and Automation (ICRA’00).
Kuffner, J., Nishiwaki, K., Kagami, S., Inaba, M., and In-
oue, H. (2003). Motion planning for humanoid robots.
In Int’l Symp. Robotics Research (ISRR’03).
Latombe, J. (1991). Robot Motion Planning (4th edition).
Kluwer Academic.
LaValle, S. (1998). Rapidly-exploring random trees: A new
tool for path planning. Technical Report 98-11, Dept.
of Computer Science, Iowa State University.
LaValle, S. (2004). Planning Algorithms. [on-line book].
http://msl.cs.uiuc.edu/planning/.
LaValle, S. and Kuffner, J. (1999). Randomized kinody-
namic planning. In Int. Conf. on Robotics and Au-
tomation (ICRA’99).
LaValle, S. and Kuffner, J. (2000). Rapidly-exploring ran-
dom trees: Progress and prospects. In Workshop on
the Algorithmic Foundations of Robotics (WAFR’00).
Lindemann, S. and LaValle, S. (2004). Incrementally reduc-
ing dispersion by increasing Voronoi bias in RRTs. In
Int. Conf. on Robotics and Automation (ICRA’04).
Lindemann, S. R. and LaValle, S. M. (2003). Current issues
in sampling-based motion planning. In Int. Symp. on
Robotics Research (ISRR’03).
Lozano-Pérez, T. (1983). Spatial Planning: A Configuration
Space Approach. In Trans. on Computers.
Russell, S. (2002). Rationality and Intelligence. In Press,
O. U., editor, Common sense, reasoning, and rational-
ity.
Russell, S. and Norvig, P. (2003). Artificial Intelligence, A
Modern Approach (2ème édition). Prentice Hall.
ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics
106

Schwartz, J. and Sharir, M. (1983). On the piano movers
problem:I, II, III, IV, V. Technical report, New York
University, Courant Institute, Department of Com-
puter Sciences.
Simov, B., LaValle, S., and Slutzki, G. (2002). A com-
plete pursuit-evasion algorithm for two pursuers using
beam detection. In Int. Conf. on Robotics and Automa-
tion (ICRA’02).
Svestka, P. (1997). Robot Motion Planning using Proba-
bilistic Roadmaps. PhD thesis, Utrecht University.
Tovar, B., LaValle, S., and Murrieta, R. (2003). Optimal
navigation and object finding without geometric maps
or localization. In Int. Conf. on Robotics and Automa-
tion (ICRA’03).
Williams, B. C., B.C., Kim, P., Hofbaur, M., How, J., Ken-
nell, J., Loy, J., Ragno, R., Stedl, J., and Walcott, A.
Model-based reactive programming of cooperative ve-
hicles for mars exploration. In Int. Symp. on Artificial
Intelligence, Robotics and Automation in Space, page
2001.
Yershova, A., Jaillet, L., Simeon, T., and LaValle, S. M.
(2005). Dynamic-domain rrts: Efficient exploration
by controlling the sampling domain. In Int. Conf. on
Robotics and Automation (ICRA’05).
RSRT: RAPIDLY EXPLORING SORTED RANDOM TREE - Online Adapting RRT to Reduce Computational Solving
Time while Motion Planning in Wide Configuration Spaces
107